将4个相同的白球、5个相同的黑球、6个相同的红球放入4个不同的盒子中的3个中,使得有一个空盒且其他盒子中球的颜色齐全的不同放法有多少种?
如图1矩形APCD中,AD=2AP,B为PC的中点,将三角形APB折沿AB折起,使得PD=PC,如图2.
(1)若E为PD中点,证明CE//平面APB;
(2)证明:平面APB 平面ABCD.
平面ABCD.
已知圆C: ,直线
,直线 :
:  .
.
(1)求证:对 ,直线
,直线 与圆C总有两个不同的交点;
与圆C总有两个不同的交点;
(2)若直线 被圆C截得的弦长最小时,求直线
被圆C截得的弦长最小时,求直线 的方程.
的方程.
如图,矩形ABCD所在的平面与三角形CDE所在的平面交于CD, AE 平面CDE.
平面CDE.
求证:(1)AB//平面CDE;
(2)CD 平面ADE.
平面ADE.
求斜率为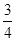 且与坐标轴围成的三角形面积是6的直线方程.
且与坐标轴围成的三角形面积是6的直线方程.
在平面直角坐标系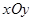 中,
中, 的边
的边 所在的直线方程是
所在的直线方程是 ,
,
(1)如果一束光线从原点 射出,经直线
射出,经直线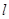 反射后,经过点
反射后,经过点 ,求反射后光线所在直线的方程;
,求反射后光线所在直线的方程;
(2)如果在 中,
中,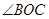 为直角,求
为直角,求 面积的最小值.
面积的最小值.