
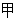
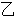
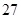
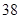
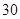
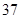
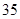
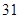

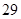
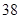
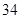
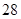
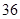 为了选拔参加奥运会选手,教练员对甲,乙自行车运动员进行测试,测得他们的最大速度
为了选拔参加奥运会选手,教练员对甲,乙自行车运动员进行测试,测得他们的最大速度
的数据如下表所示(单位m/s)
请判断谁参加这项重大比赛更合适,并阐述理由。
(本小题满分13分)
已知椭圆 的短轴长为
的短轴长为 ,且与抛物线
,且与抛物线 有共同的焦点,椭圆
有共同的焦点,椭圆 的左顶点为A,右顶点为
的左顶点为A,右顶点为 ,点
,点 是椭圆
是椭圆 上位于
上位于 轴上方的动点,直线
轴上方的动点,直线 ,
, 与直线
与直线 分别交于
分别交于 两点.
两点.
(I)求椭圆 的方程;
的方程;
(Ⅱ)求线段 的长度的最小值;
的长度的最小值;
(Ⅲ)在线段 的长度取得最小值时,椭圆
的长度取得最小值时,椭圆 上是否存在一点
上是否存在一点 ,使得
,使得 的面积为
的面积为 ,若存在求出点
,若存在求出点 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
(本小题满分13分)
已知等比数列 的公比
的公比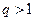 ,
,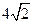 是
是 和
和 的一个等比中项,
的一个等比中项,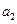 和
和 的等差中项为
的等差中项为 ,若数列
,若数列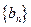 满足
满足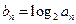 (
(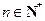 ).
).
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)求数列 的前
的前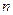 项和
项和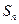 .
.
(本小题满分14分)
如图,四棱锥 中,
中,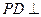 平面
平面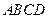 ,底面
,底面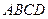 为矩形,
为矩形, ,
,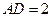 ,
, 为
为 的中点.
的中点.
(Ⅰ)求证: ;
;
(Ⅱ)求三棱锥 的体积;
的体积;
(Ⅲ) 边上是否存在一点
边上是否存在一点 ,使得
,使得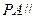 平面
平面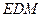 ,若存在,求出
,若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.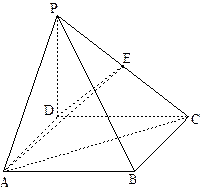
(本小题满分13分)
随机抽取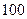 名学生,测得他们的身高(单位:
名学生,测得他们的身高(单位: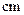 ),按照区间
),按照区间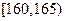 ,
,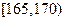 ,
,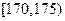 ,
,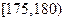 ,
,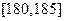 分组,得到样本身高的频率分布直方图(如图).
分组,得到样本身高的频率分布直方图(如图).
(Ⅰ)求频率分布直方图中 的值及身高在
的值及身高在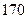
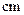 以上的学生人数;
以上的学生人数;
(Ⅱ)将身高在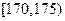 ,
,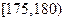 ,
,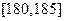 区间内的学生依次记为
区间内的学生依次记为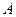 ,
,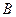 ,
,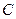 三个组,用分层抽样的方法从三个组中抽取
三个组,用分层抽样的方法从三个组中抽取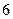 人,求从这三个组分别抽取的学生人数;
人,求从这三个组分别抽取的学生人数;
(Ⅲ)在(Ⅱ)的条件下,要从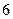 名学生中抽取
名学生中抽取 人,用列举法计算
人,用列举法计算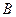 组中至少有
组中至少有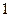 人被抽中的概率.
人被抽中的概率.
(本小题满分13分)
在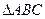 中,角
中,角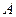 ,
,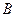 ,
, 所对的边分别为
所对的边分别为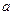 ,
,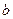 ,
, ,且
,且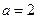 ,
, .
.
(Ⅰ)若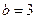 ,求
,求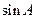 的值;
的值;
(Ⅱ)若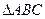 的面积
的面积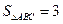 ,求
,求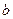 ,
, 的值21.世纪教
的值21.世纪教