、已知 是平面坐标内三点,其坐标分别为
是平面坐标内三点,其坐标分别为 ,
, ,
,
(Ⅰ)求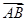 .
. 和
和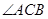 大小,并判断
大小,并判断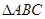 形状;
形状;
(Ⅱ)若 为
为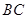 中点,求
中点,求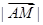 .
.
(本小题满分14分)已知一个数列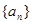 的各项都是1或2.首项为1,且在第
的各项都是1或2.首项为1,且在第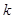 个1和第
个1和第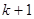 个1之间有
个1之间有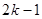 个2,即1,2,1,2,2,2,1,2,2,2,2,2,1,….记数列的前
个2,即1,2,1,2,2,2,1,2,2,2,2,2,1,….记数列的前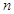 项的和为
项的和为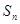 .参考:31×32=992,32×33=1056,44×45=1980,45×46=2070
.参考:31×32=992,32×33=1056,44×45=1980,45×46=2070
(I)试问第10个1为该数列的第几项?
(II)求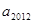 和
和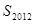 ;
;
(III)是否存在正整数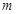 ,使得
,使得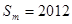 ?如果存在,求出
?如果存在,求出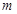 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
(本小题满分12分)美国华尔街的次贷危机引起的金融风暴席卷全球,低迷的市场造成产品销售越来越难,为此某厂家举行大型的促销活动,经测算该产品的销售量P万件(生产量与销售量相等)与促销费用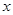 万元满足
万元满足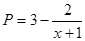 ,已知生产该产品还需投入成本
,已知生产该产品还需投入成本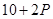 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为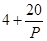 元/万件.
元/万件.
(Ⅰ)将该产品的利润 万元表示为促销费用
万元表示为促销费用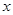 万元的函数;
万元的函数;
(Ⅱ)促销费用投入多少万元时,厂家的利润最大。
(本小题满分12分)某炮兵阵地位于地面A处,两观察所分别位于地面点C和D处, 已知CD=6000m,∠ACD=45°,∠ADC=75°, 目标出现于地面点B处时,测得∠BCD=30°,∠BDC=15°(如图),求炮兵阵地到目标的距离.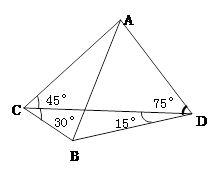
已知不等式 的解集为
的解集为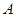 ,不等式
,不等式 的解集为
的解集为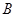 .
.
(Ⅰ) 求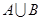 ;
;
(Ⅱ)若不等式 的解集为
的解集为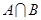 ,求
,求 的值.
的值.
(本小题满分12分)已知等差数列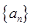 满足:
满足: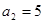 ,
,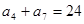 ,
,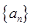 的前n项和为
的前n项和为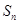 .
.
(Ⅰ)求通项公式 及前n项和
及前n项和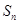 ;
;
(Ⅱ)令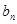 =
=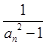 (n
(n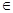 N*),求数列
N*),求数列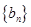 的前n项和
的前n项和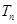 .
.