如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO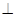 底面ABCD,E是PC的中点.
底面ABCD,E是PC的中点.
求证:(1)PA∥平面BDE;
(2)平面EBD⊥平面PAC
对于项数为m的有穷数列数集
,记
(
),即
为
中的最大值,并称数列
是
的控制数列.如1,3,2,5,5的控制数列是1,3,3,5,5.
(1)若各项均为正整数的数列
的控制数列为2,3,4,5,5,写出所有的
;
(2)设
是
的控制数列,满足
(
为常数,
).求证:
(
);
(3)设
,常数
.若
,
是
的控制数列,求
.
在平面直角坐标系
中,已知双曲线
.
(1)设
是
的左焦点,
是
右支上一点. 若
,求过
点的坐标;
(2)过
的左顶点作
的两条渐近线的平行线,求这两组平行线围成的平行四边形的
面积;
(3)设斜率为
的直线
交
于
、
两点,若
与圆
相切,
求证:
;
海事救援船对一艘失事船进行定位:以失事船的当前位置为原点,以正北方向为 轴正方向建立平面直角坐标系(以1海里为单位长度),则救援船恰在失事船的正南方向12海里 处,如图.现假设:①失事船的移动路径可视为抛物线 ;②定位后救援船即刻沿直线匀速前往救援;③救援船出发 小时后,失事船所在位置的横坐标为 .

(1)当
时,写出失事船所在位置
的纵坐标. 若此时两船恰好会合,求救援船速度的大小和方向;
(2)问救援船的时速至少是多少海里才能追上失事船?
已知函数
.
(1)若
,求
的取值范围;
(2)若
是以2为周期的偶函数,且当
时,有
,求函数
的反函数.
如图,在三棱锥 中, , 是 的中点.已知 , , , .求:

(1)三棱锥
的体积;
(2)异面直线
与
所成的角的大小(结果用反三角函数值表示).