海事救援船对一艘失事船进行定位:以失事船的当前位置为原点,以正北方向为 轴正方向建立平面直角坐标系(以1海里为单位长度),则救援船恰在失事船的正南方向12海里 处,如图.现假设:①失事船的移动路径可视为抛物线 ;②定位后救援船即刻沿直线匀速前往救援;③救援船出发 小时后,失事船所在位置的横坐标为 .

(1)当
时,写出失事船所在位置
的纵坐标. 若此时两船恰好会合,求救援船速度的大小和方向;
(2)问救援船的时速至少是多少海里才能追上失事船?
如图,三棱柱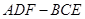 中,所有棱长均为2,
中,所有棱长均为2,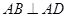 ,
,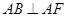 ,平面
,平面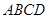 ⊥平面
⊥平面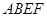 ,
, 分别是
分别是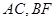 上的中点.
上的中点.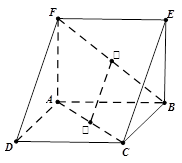
(1)求证: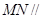 平面
平面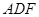 ;
;
(2)求直线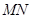 与平面
与平面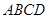 所成角的大小.
所成角的大小.
为适应2012年3月23日公安部交通管理局印发的《加强机动车驾驶人管理指导意见》,某驾校将小型汽车驾照考试科目二的培训测试调整为:从10个备选测试项目中随机抽取4个,只有选中的4个项目均测试合格,科目二的培训才算通过.已知甲对10个测试项目测试合格的概率均为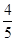 ;乙对其中8个测试项目完全有合格把握,而另2个测试项目却根本不会.
;乙对其中8个测试项目完全有合格把握,而另2个测试项目却根本不会.
(1)求甲恰有2个测试项目合格的概率;
(2)记乙的测试项目合格数为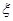 ,求
,求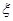 的分布列及数学期望
的分布列及数学期望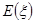 .
.
已知函数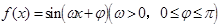 为偶函数,且其图象上相邻两对称轴之间的距离为
为偶函数,且其图象上相邻两对称轴之间的距离为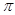 .
.
(1)求函数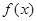 的表达式.
的表达式.
(2)若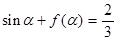 ,求
,求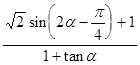 的值.
的值.
函数y=2cos(ωx+θ)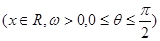
的图象与y轴交于点(0,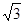 ),且该函数的最小正周期为π.
),且该函数的最小正周期为π.
(1)求θ和ω的值;
(2)已知点A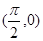 ,点P是该函数图象上一点,点Q(x0,y0)是PA的中点,当y0=
,点P是该函数图象上一点,点Q(x0,y0)是PA的中点,当y0=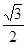 ,x0∈
,x0∈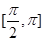 时,求x0的值.
时,求x0的值.
已知函数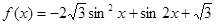 .
.
(1)求函数f(x)的最小正周期和单调增区间;
(2)在给出的直角坐标系中,画出函数y=f(x)在区间[0,π]上的图象.