本题共有2个小题,第1小题满分6分,第2小题满分8分.
如图1, ,
, 是某地一个湖泊的两条互相垂直的湖堤,线段
是某地一个湖泊的两条互相垂直的湖堤,线段 和曲线段
和曲线段 分别是湖泊中的一座栈桥和一条防波堤。为观光旅游的需要,拟过栈桥
分别是湖泊中的一座栈桥和一条防波堤。为观光旅游的需要,拟过栈桥 上某点
上某点 分别修建与
分别修建与 ,
, 平行的栈桥
平行的栈桥 、
、 ,且以
,且以 、
、 为边建一个跨越水面的三角形观光平台
为边建一个跨越水面的三角形观光平台 。建立如图2所示的直角坐标系,测得线段
。建立如图2所示的直角坐标系,测得线段 的方程是
的方程是 ,曲线段
,曲线段 的方程是
的方程是 ,设点
,设点 的坐标为
的坐标为 ,记
,记 。(题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度)
。(题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度)
(1)求 的取值范围;
的取值范围;
(2)试写出三角形观光平台 面积
面积 关于
关于 的函数解析式,并求出该面积的最小值
的函数解析式,并求出该面积的最小值
求平行于直线 ,且与它的距离为
,且与它的距离为 的直线的方程。
的直线的方程。
(本小题满分12分)
已知函数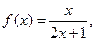 数列
数列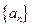 满足
满足 .
.
(1)求证:数列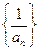 是等差数列;
是等差数列;
(2)若数列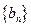 前
前 项和为
项和为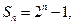 记
记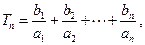 求
求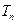 .
.
(本小题满分12分)
在海岸A处,发现北偏东 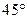 方向,距离A为
方向,距离A为 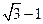
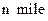 的B处有一艘走私船,在A处北偏西
的B处有一艘走私船,在A处北偏西 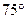 方向,距离A为
方向,距离A为 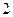
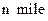 的C处有一艘缉私艇奉命以
的C处有一艘缉私艇奉命以 
 的速度追截走私船,此时,走私船正以
的速度追截走私船,此时,走私船正以 
 的速度从B处向北偏东
的速度从B处向北偏东 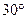 方向逃窜,问缉私艇沿什么方向行驶才能最快追上走私船?并求出所需时间.(本题解题过程中请不要使用计算器,以保证数据的相对准确和计算的方便)
方向逃窜,问缉私艇沿什么方向行驶才能最快追上走私船?并求出所需时间.(本题解题过程中请不要使用计算器,以保证数据的相对准确和计算的方便)
|
|
(本小题满分12分)
某汽车公司购买了4辆大客车,每辆200万元,用于长途客运,预计每辆车每年收入约100万元,每辆车每年各种费用约为16万元,且从第二年开始每年比上一年所需费用要增加16万元.
(1)写出4辆车运营的总利润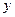 (万元)与运营年数
(万元)与运营年数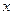
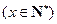 的函数关系式;
的函数关系式;
(2)这4辆车运营多少年,可使年平均运营利润最大?
(本小题满分12分)
在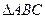 中,内角
中,内角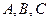 对边的边长分别是
对边的边长分别是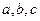 ,且
,且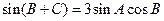 .
.
(1)求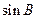 的值;
的值;
(2)若 ,且
,且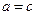 ,求
,求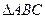 的面积.
的面积.