(本小题满分12分)如图,在三棱锥 中,
中, 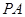 、
、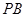 、
、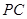 两两垂直,且
两两垂直,且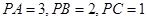 .设
.设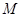 是底面
是底面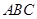 内一点,定义
内一点,定义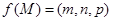 ,其中
,其中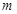 、
、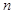 、
、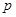 分别是三棱锥
分别是三棱锥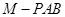 、 三棱锥
、 三棱锥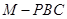 、三棱锥
、三棱锥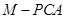 的体积.已知
的体积.已知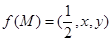 .
.
(Ⅰ)求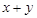 的值;
的值;
(Ⅱ)若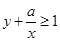 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
如图,已知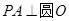 所在的平面,
所在的平面,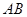 是
是 的直径,
的直径,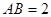 ,
, 上的一点,且
上的一点,且 ,
, ,
,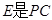 中点,
中点, 的中点.
的中点.
(1)求证: //面
//面 ;
;
(2)求证: ;
;
(3)求三棱锥 的体积
的体积
某校高二的一个班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:
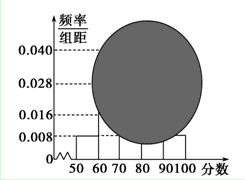
(1)求分数在[50,60)的频率及全班人数;
(2)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(3)试用此频率分布直方图估计这组数据的众数和平均数.
圆 的圆心在直线
的圆心在直线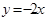 上,且与直线
上,且与直线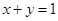 相切于点
相切于点 ,
,
(1)试求圆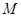 的方程;
的方程;
(2)从点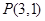 发出的光线经直线
发出的光线经直线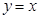 反射后可以照在圆
反射后可以照在圆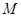 上,试求发出光线所在直线的斜率取值范围.
上,试求发出光线所在直线的斜率取值范围.
下列程序的输出结果构成了数列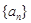 的前10项.试根据该程序给出的数列关系,
的前10项.试根据该程序给出的数列关系,
(1)求数列的第3项 和第4项
和第4项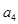 ;
;
(2)写出该数列的递推公式,并求出其通项公式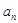 ;
;
已知直线 :
: ,
,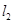 :
: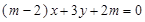 ,求当
,求当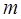 为何值时,
为何值时, 与
与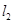 :(1)平行;(2)相交;(3)垂直.
:(1)平行;(2)相交;(3)垂直.