某工厂有甲、乙两个生产小组,每个小组各有四名工人,某天该厂每位工人的生产情况如下表.
| |
员工号 |
1 |
2 |
3 |
4 |
| 甲组 |
件数 |
9 |
11 |
1l |
9 |
| |
员工号 |
1 |
2 |
3 |
4 |
| 乙组 |
件数 |
b 9 |
8 |
10 |
9 |
(1)用茎叶图表示两组的生产情况;
(2)求乙组员工生产件数的平均数和方差;
(3)分别从甲、乙两组中随机选取一名员工的生产件数,求这两名员工的生产总件数为19的概率.
(注:方差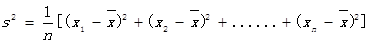 ,其中
,其中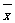 为x1,x2,…,xn的平均数)
为x1,x2,…,xn的平均数)
(1)已知两个等比数列
,满足
,若数列
唯一,求
的值;
(2)是否存在两个等比数列
,使得
成公差不为 的等差数列?若存在,求
的通项公式;若不存在,说明理由.
的等差数列?若存在,求
的通项公式;若不存在,说明理由.
设
.
(1)如果
在
处取得最小值
,求
的解析式;
(2)如果
,
的单调递减区间的长度是正整数,试求
和
的值.(注:区间
的长度为
)
已知过抛物线
的焦点,斜率为
的直线交抛物线于
两点,且
.
(1)求该抛物线的方程;
(2)
为坐标原点,
为抛物线上一点,若
,求
的值.
如图,在
中,
,
,
为
边上一动点,
交
于点
,现将
沿
翻折至
,使平面
.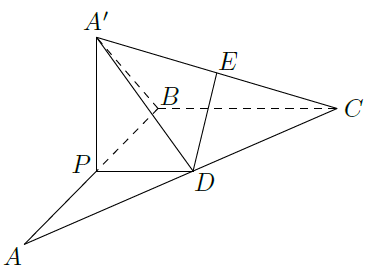
(1)当棱锥
的体积最大时,求
的长;
(2)若点
为
的中点,E为
的中点,求证:
.
在
中,
的对边分别是
,已知
.
(1)求
的值;
(2)若
,求边
的值.