已知函数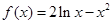 .
.
(I) 求函数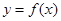 在
在 上的最大值.
上的最大值.
(II)如果函数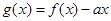 的图像与
的图像与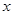 轴交于两点
轴交于两点 、
、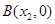 ,且
,且 .
. 是
是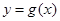 的导函数,若正常数
的导函数,若正常数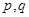 满足
满足 .
.
求证: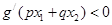 .
.
(满分12分)设函数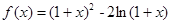 。
。
(Ⅰ)若在定义域内存在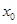 ,而使得不等式
,而使得不等式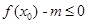 能成立,求实数
能成立,求实数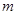 的最小值;
的最小值;
(Ⅱ)若函数 在区间
在区间 上恰有两个不同的零点,求实数
上恰有两个不同的零点,求实数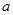 的取值范围。
的取值范围。
(满分12分)已知:正方体 中,棱长
中,棱长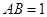 ,
,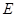 、
、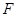 分别为
分别为 、
、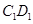 的中点,
的中点, 、
、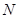 是
是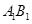 、
、 的中点,
的中点,
(1)求证: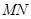 //平面
//平面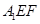 ;
;
(2)求: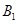 到平面
到平面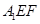 的距离。
的距离。
(满分10分)(Ⅰ) 设椭圆方程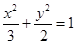 的左、右顶点分别为
的左、右顶点分别为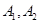 ,点M是椭圆上异于
,点M是椭圆上异于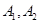 的任意一点,设直线
的任意一点,设直线 的斜率分别为
的斜率分别为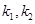 ,求证
,求证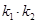 为定值并求出此定值;
为定值并求出此定值;
(Ⅱ)设椭圆方程 的左、右顶点分别为
的左、右顶点分别为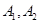 ,点M是椭圆上异于
,点M是椭圆上异于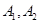 的任意一点,设直线
的任意一点,设直线 的斜率分别为
的斜率分别为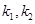 ,利用(Ⅰ)的结论直接写出
,利用(Ⅰ)的结论直接写出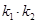 的值。(不必写出推理过程)
的值。(不必写出推理过程)
(本小题满分14分)
二次函数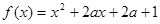 .
.
(1)若对任意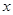
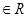 有
有 恒成立,求实数
恒成立,求实数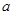 的取值范围;
的取值范围;
(2)讨论函数 在区间
在区间 上的单调性;
上的单调性;
(3)若对任意的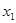 ,
,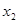
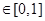 有
有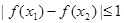 恒成立,求实数
恒成立,求实数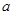 的取值范围.
的取值范围.
已知椭圆 过点
过点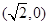 ,且离心率为
,且离心率为 .
.
(1)求椭圆 的方程;
的方程;
(2) 为椭圆
为椭圆 的左右顶点,点
的左右顶点,点 是椭圆
是椭圆 上异于
上异于 的动点,直线
的动点,直线 分别交直线
分别交直线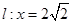 于
于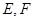 两点.
两点.
证明:以线段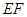 为直径的圆恒过
为直径的圆恒过 轴上的定点.
轴上的定点.