.(本小题满分l 3分)某种商品原来每件售价为25元,年销售量8万件.
(I)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收人不低于原收入,该商品每件定价最多为多少元?
(Ⅱ)为了扩大该商品的影响力,提高年销售量.公司决定明年对该商品进行全面技术革新和营销策略改革,并提高定价到x元.公司拟投入 (x2—600)万元作为技改费用,投入50万元作为固定宣传费用,投入
(x2—600)万元作为技改费用,投入50万元作为固定宣传费用,投入 x万元作为浮动宣传费用.试问:当该商品明年的销售量a至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
x万元作为浮动宣传费用.试问:当该商品明年的销售量a至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
数列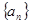 中,
中, 且满足
且满足

⑴求数列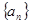 的通项公式;
的通项公式;
⑵设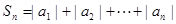 ,求
,求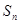 ;
;
⑶设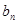 =
=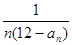
 ,是否存在最大的整数
,是否存在最大的整数 ,使得对任意
,使得对任意 ,均有
,均有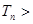
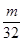 成立?若存在,求出
成立?若存在,求出 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
如图,正四棱柱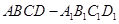 中,
中,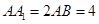 ,点
,点 在
在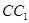 上且
上且 .
.
(Ⅰ)证明: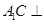 平面
平面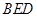 ;
;
(Ⅱ)求二面角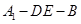 的大小.
的大小.
一个口袋中有大小相同的2个白球和4个黑球,每次从袋中随机地摸出1个球,并换入1只相同大小的黑球,这样继续下去,求:
(I)摸2次摸出的都是白球的概率;
(II)第3次摸出的是白球的概率。
已知函数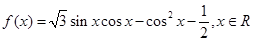 . (Ⅰ) 求函数
. (Ⅰ) 求函数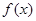 的最小值和最小正周期;(Ⅱ)已知
的最小值和最小正周期;(Ⅱ)已知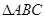 内角
内角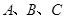 的对边分别为
的对边分别为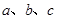 ,且
,且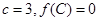 ,若向量
,若向量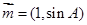 与
与 共线,求
共线,求 的值.
的值.
(本题满分14分)已知函数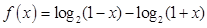 .
.
(1)求函数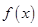 的定义域;
的定义域;
(2)判断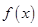 的奇偶性;
的奇偶性;
(3)方程 是否有根?如果有根
是否有根?如果有根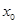 ,请求出一个长度为
,请求出一个长度为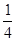 的区间
的区间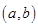 ,使
,使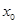
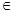
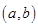 ;如果没有,请说明理由?(注:区间的长度为
;如果没有,请说明理由?(注:区间的长度为 ).
).