已知圆 :
: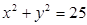 :
:
(Ⅰ)直线 经过点
经过点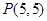 ,其斜率为
,其斜率为 ,
, 与圆
与圆 交点分别为
交点分别为 ,
,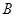 ,若
,若 ,求
,求 的值;
的值;
(Ⅱ)点 是圆
是圆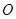 上除去与
上除去与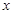 轴交点中的任意一点,过点
轴交点中的任意一点,过点 作
作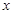 轴的垂线段
轴的垂线段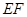 ,
,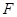 为垂足,当点
为垂足,当点 在圆
在圆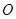 上运动时,求线段
上运动时,求线段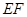 中点
中点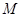 的轨迹方程.
的轨迹方程.
(1)一个半径为r的扇形,若它的周长等于弧所在的半圆的长,那么扇形的圆心角是多少弧度?是多少度?扇形的面积是多少?
(2)一扇形的周长为20 cm,当扇形的圆心角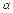 等于多少弧度时,这个扇形的面积最大?
等于多少弧度时,这个扇形的面积最大?
在单位圆中画出适合下列条件的角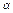 的终边的范围,并由此写出角
的终边的范围,并由此写出角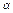 的集合:
的集合:
(1)sin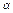 ≥
≥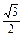 ;(2)cos
;(2)cos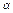 ≤
≤ .
.
(1)一个半径为r的扇形,若它的周长等于弧所在的半圆的长,那么扇形的圆心角是多少弧度?是多少度?扇形的面积是多少?
(2)一扇形的周长为20 cm,当扇形的圆心角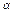 等于多少弧度时,这个扇形的面积最大?
等于多少弧度时,这个扇形的面积最大?
若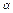 是第二象限的角,试分别确定2
是第二象限的角,试分别确定2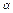 ,
, ,
, 的终边所在位置.
的终边所在位置.
已知cos( +
+ )=-
)=- ,且
,且 是第四象限角,计算:
是第四象限角,计算:
(1)sin(2 -
- );
);
(2)  (n∈Z).
(n∈Z).