在直角坐标系 中,点P到两点
中,点P到两点 ,
, 的距离之和等于4,设点P的轨迹为
的距离之和等于4,设点P的轨迹为 ,直线
,直线 与C交于A,B两点.
与C交于A,B两点.
(Ⅰ)写出C的方程;
(Ⅱ)若

 ,求k的值;
,求k的值;
(Ⅲ)若点A在第一象限,证明:当k>0时,恒有| |>|
|>| |.
|.
(本小题满分12分)已知数列
(1)求证数列 是等差数列,并求数列
是等差数列,并求数列 的通项公式;
的通项公式;
(2)令 , 求数列
, 求数列 的前
的前 项和
项和 .
.
(本小题满分14分)已知函数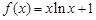 ,
,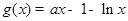
(Ⅰ)求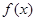 的最小值;
的最小值;
(Ⅱ)讨论函数 的单调性;
的单调性;
(Ⅲ)是否存在常数 ,使
,使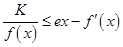 恒成立,若存在,求出
恒成立,若存在,求出 的最大值,若不存在,说明理由.
的最大值,若不存在,说明理由.
(本小题满分12分)经过多年的运作,“双十一”抢购活动已经演变成为整个电商行业的大型集体促销盛宴. 为迎接2014年“双十一”网购狂欢节,某厂商拟投入适当的广告费,对网上所售产品进行促销. 经调查测算,该促销产品在“双十一”的销售量P万件与促销费用x万元满足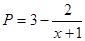 (其中
(其中 ,a为正常数).已知生产该批产品P万件还需投入成本
,a为正常数).已知生产该批产品P万件还需投入成本 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为 元/件,假定厂家的生产能力完全能满足市场的销售需求.
元/件,假定厂家的生产能力完全能满足市场的销售需求.
(Ⅰ)将该产品的利润y万元表示为促销费用x万元的函数;
(Ⅱ)促销费用投入多少万元时,厂家的利润最大?
(本小题满分12分)已知椭圆E的方程: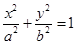 (
( ),它的两个焦点为
),它的两个焦点为 ,P为椭圆的一点(点
,P为椭圆的一点(点 在第三象限上), 且
在第三象限上), 且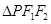 的周长为
的周长为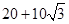 ,
,
(Ⅰ)求椭圆E的方程;
(Ⅱ)若以点P为圆心的圆过椭圆的左顶点M与点 , MP交圆P与另一点N,若点A在椭圆E上,使得
, MP交圆P与另一点N,若点A在椭圆E上,使得 ,求点A的坐标.
,求点A的坐标.
(本小题满分12分)已知等差数列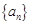 的前
的前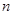 项和为
项和为 ,且
,且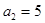 ,
,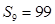 .
.
(Ⅰ)求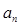 及
及 ;
;
(Ⅱ)若数列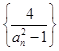 的前
的前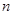 项和
项和 ,试求
,试求 并证明不等式
并证明不等式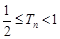 成立.
成立.