在几何体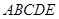 中,
中,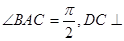 平面
平面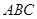 ,
,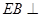 平面
平面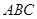 ,
, .
.
(1)设平面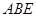 与平面
与平面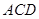 的交线为直线
的交线为直线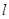 ,求证:
,求证: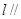 平面
平面 ;
;
(2)设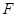 是
是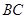 的中点,求证:平面
的中点,求证:平面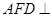 平面
平面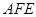 ;
;
(3)求几何体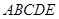 的体积.
的体积.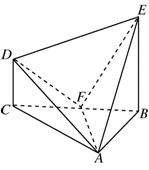
已知关于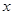 的二次函数
的二次函数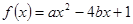 ,
,
(1)设集合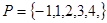 ,和
,和 分别从集合
分别从集合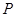 和
和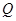 中随机取出一个数作为
中随机取出一个数作为 和
和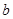 ,求函数
,求函数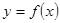 在区间
在区间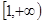 上是增函数的概率;
上是增函数的概率;
(2)设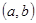 是区域
是区域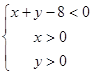
 的随机点,求函数
的随机点,求函数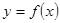 在区间
在区间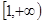 上是增函数的概率。
上是增函数的概率。
已知等比数列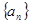 的公比
的公比 ,前
,前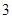 项和
项和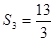 .
.
(1)求数列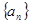 的通项公式;
的通项公式;
(2)若函数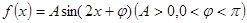 在
在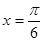 处取得最大值,且最大值为
处取得最大值,且最大值为 ,求函数
,求函数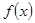 的解析式.
的解析式.
选修4-5:不等式选讲
(Ⅰ)若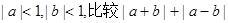 与2的大小,并说明理由;
与2的大小,并说明理由;
(Ⅱ)设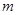 是
是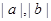 和1中最大的一个,当
和1中最大的一个,当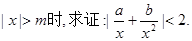
选修4-4:坐标系与参数方程
在极坐标系中,极点为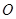 ,已知曲线
,已知曲线 :
: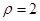 与曲线
与曲线 :
: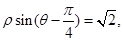 交于不同的两点
交于不同的两点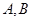 .
.
(1)求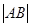 的值;
的值;
(2)求过点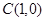 且与直线
且与直线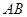 平行的直线
平行的直线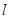 的极坐标方程.
的极坐标方程.