某日用品按行业质量标准分成五个等级,等级系数X依次为1.2.3.4.5.现从一批该日用品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如下:
| X |
1 |
2 |
3 |
4 |
5 |
| f |
a |
0.2 |
0.45 |
b |
c |
(1)若所抽取的20件日用品中,等级系数为4的恰有3件,等级系数为5的恰有2件,求a、b、c的值;
(2)在(1)的条件下,将等级系数为4的3件日用品记为x1,x2,x3,等级系数为5的2件日用品记为y1,y2,现从 这5件日用品中任取两件(假定每件日用品被取出的可能性相同),写出所有可能的结果,并求这两件日用品的等级系数恰好相等的概率.
这5件日用品中任取两件(假定每件日用品被取出的可能性相同),写出所有可能的结果,并求这两件日用品的等级系数恰好相等的概率.
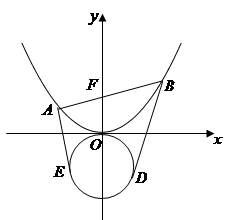
过点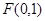 作直线
作直线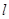 与抛物线
与抛物线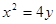 相交于两点
相交于两点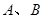 ,圆
,圆
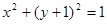
(1)若抛物线在点 处的切线恰好与圆
处的切线恰好与圆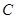 相切,求直线
相切,求直线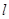 的方程;
的方程;
(2)过点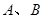 分别作圆
分别作圆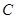 的切线
的切线 ,
,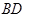 试求
试求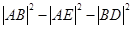 的取值范围.
的取值范围.
.(本题满分12分) 如图,PA垂直于矩形ABCD所在的平面, 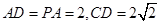 ,E、F分别是AB、PD的中点.
,E、F分别是AB、PD的中点. 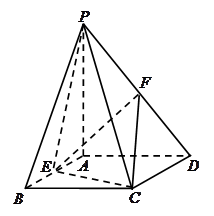
(1)求证:平面PCE 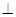 平面PCD;
平面PCD;
(2)求三棱锥P-EFC的体积.
(本题满分12分)已知数列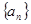 的通项公式为
的通项公式为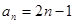 ,数列
,数列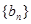 的前n项和为
的前n项和为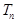 ,且满足
,且满足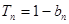
(1)求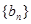 的通项公式;
的通项公式;
(2)在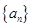 中是否存在使得
中是否存在使得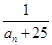 是
是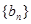 中的项,若存在,请写出满足题意的一项(不要求写出所有的项);若不存在,请说明理由.
中的项,若存在,请写出满足题意的一项(不要求写出所有的项);若不存在,请说明理由.
在极坐标中,已知圆 经过点
经过点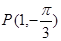 ,圆心为直线
,圆心为直线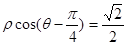 与极轴的交点,求圆
与极轴的交点,求圆 的极坐标方程.
的极坐标方程.
已知点P(4,4),圆C: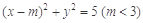 与椭圆E:
与椭圆E: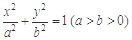 有一个公共点A(3,1),F1、F2分别是椭圆的左、右焦点,直线PF1与圆C相切.
有一个公共点A(3,1),F1、F2分别是椭圆的左、右焦点,直线PF1与圆C相切.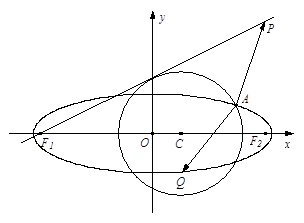
(1)求m的值与椭圆E的方程;
(2)设Q为椭圆E上的一个动点,求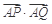 的取值范围.
的取值范围.