某高校设计了一个实验学科的实验考查方案:考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作. 规定:至少正确完成其中2题的便可提交通过.已知6道备选题中考生甲有4题能正确完成,2题不能完成;考生乙每题正确完成的概率都是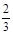 ,且每题正确完成与否互不影响. 求:
,且每题正确完成与否互不影响. 求:
(1)分别写出甲、乙两考生正确完成题数的概率分布列,并计算数学期望;
(2) 试从两位考生正确完成题数的数学期望及至少正确完成2题的概率分析比较两位考生的实验操作能力。
数列 满足:
(I)证明:数列 是单调递减数列的充分必要条件是
(II)求 的取值范围,使数列 是单调递增数列。
如图,
分别是椭圆
的左,右焦点,过点
作
轴的垂线交椭圆的上半部分于点P,过点
作直线
的垂线交直线
于点
;
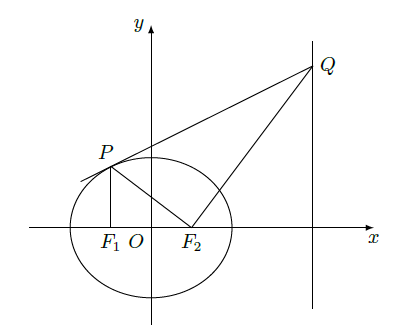
(I)若点
的坐标为(4,4);求椭圆
的方程;
(II)证明:直线
与椭圆
只有一个交点
.
设 .
(I)求
在
上的最小值;
(II)设曲线
在点
的切线方程为
;求
的值.
平面图形
如图所示,其中
是矩形,
,
,
。现将该平面图形分别沿
和
折叠,使
与
所在平面都与平面
垂直,再分别连接
,得到如图2所示的空间图形,对此空间图形解答下列问题
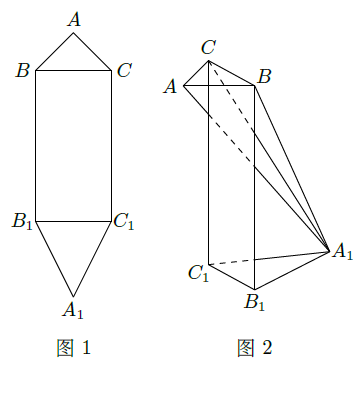
(Ⅰ)证明:
;
(Ⅱ)求
的长;
(Ⅲ)求二面角
的余弦值.
某单位招聘面试,每次从试题库随机调用一道试题,若调用的是
类型试题,则使用后该试题回库,并增补一道 类试题和一道
类试题和一道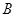 类型试题入库,此次调题工作结束;若调用的是
类型试题,则使用后该试题回库,此次调题工作结束。试题库中现共有
道试题,其中有
道
类型试题和
道
类型试题,以
表示两次调题工作完成后,试题库中
类试题的数量。
类型试题入库,此次调题工作结束;若调用的是
类型试题,则使用后该试题回库,此次调题工作结束。试题库中现共有
道试题,其中有
道
类型试题和
道
类型试题,以
表示两次调题工作完成后,试题库中
类试题的数量。
(Ⅰ)求
的概率;
(Ⅱ)设
,求
的分布列和均值(数学期望)。