已知函数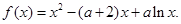 其中常数
其中常数
(1)当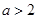 时,求函数
时,求函数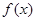 的单调递增区间;
的单调递增区间;
(2)当 时,给出两类直线:
时,给出两类直线: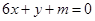 与
与 ,其中
,其中 为常数,判断这两类直线中是否存在
为常数,判断这两类直线中是否存在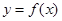 的切线,若存在,求出相应的
的切线,若存在,求出相应的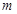 或
或 的值,若不存在,说明理由.
的值,若不存在,说明理由.
(3)设定义在 上的函数
上的函数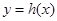 在点
在点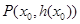 处的切线方程为
处的切线方程为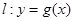 ,当
,当 若
若 在
在 内恒成立,则称
内恒成立,则称 为函数
为函数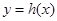 的“类对称点”,当
的“类对称点”,当 时,试问
时,试问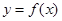 是否存在“类对称点”,若存在,请至少求出一个“类对称点”
是否存在“类对称点”,若存在,请至少求出一个“类对称点” 的横坐标,若不存在,说明理由.
的横坐标,若不存在,说明理由.
某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在(29.94,30.06)的零件为优质品。从两个分厂生产的零件中各抽出500件,量其内径尺寸,的结果如下表:
甲厂:
(1)试分别估计两个分厂生产的零件的优质品率;
(2)由于以上统计数据填下面 列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”。
列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”。
| 甲 厂 |
乙 厂 |
合计 |
|
| 优质品 |
|||
| 非优质品 |
|||
| 合计 |
附: ,
,

 .
.
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量 (吨)与相应的生产能耗
(吨)与相应的生产能耗 (吨标准煤)的几组对照数据:
(吨标准煤)的几组对照数据:
 |
 |
 |
 |
 |
 |
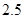 |
 |
 |
 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,求出 关于
关于 的线性回归方程
的线性回归方程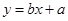 ;
;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤? (参考公式见卷首,参考数值: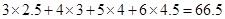 ).
).
已知函数
(1)求函数 的单调区间;
的单调区间;
(2)若 恒成立,试确定实数k的取值范围;
恒成立,试确定实数k的取值范围;
(3)证明:
① 上恒成立
上恒成立
②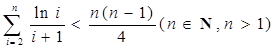
已知数列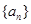 的通项公式为
的通项公式为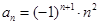 ,其前
,其前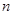 项和为
项和为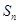 ,
,
(1)求 并猜想
并猜想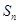 的值;
的值;
(2)用数学归纳法证明(1)中所猜想的结论.
若函数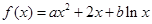 在
在 和
和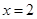 处取得极值,
处取得极值,
(1)求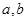 的值;
的值;
(2)求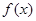 在
在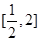 上的最大值和最小值.
上的最大值和最小值.