下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量
(吨)与相应的生产能耗
(吨标准煤)的几组对照数据：
|
 |
 |
 |
 |
| |
 |
|
|
 |
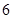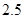(1)请画出上表数据的散点图；
(2)请根据上表提供的数据，求出关于的线性回归方程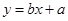
；
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤．试根据(2)求出的线性回归方程，预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤? (参考公式见卷首，参考数值：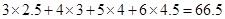
).
已知椭圆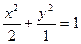
的左右焦点分别为F1,F2，若过点P（0，-2）及F1的直线交椭圆于A,B两点，求⊿ABF2的面积
(本题满分12分)已知点A（-2，0），B（2，0），动点P满足：
，且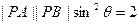
. （I）求动点P的轨迹G的方程；（II）过点B的直线
与轨迹G交于两点M，N.试问在x轴上是否存在定点C ,使得
为常数.若存在，求出点C的坐标；若不存在，说明理由.
已知函数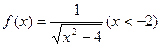
.(Ⅰ) 求f –1(x)；(Ⅱ) 若数列{an}的首项为a1=1，
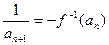(nÎN+)，求{an}的通项公式an；(Ⅲ) 设bn=an+12+an+22+¼+a2n+12，是否存在最小的正整数k，使对于任意nÎN+有bn<
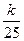成立.若存在，求出k的值；若不存在，说明理由.
2008年中国北京奥运会吉祥物由5个“中国福娃”组成，分别叫贝贝、晶晶、欢欢、迎迎、妮妮.现有8个相同的盒子，每个盒子中放一只福娃，每种福娃的数量如下表：
| 福娃名称 |
贝贝 |
晶晶 |
欢欢 |
迎迎 |
妮妮 |
| 数量 |
1 |
1 |
1 |
2 |
3 |
从中随机地选取5只.（I）求选取的5只恰好组成完整“奥运吉祥物”的概率；
（II）若完整地选取奥运会吉祥物记10分；若选出的5只中仅差一种记8分；差两种记6分；以此类推. 设ξ表示所得的分数，求ξ的分布列及数学期望.
已知定义在正实数集上的函数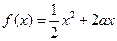
，
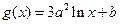，其中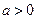
. 设两曲线
，
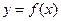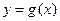有公共点，且在该点处的切线相同.（I）用
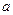表示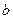
；（II）求证：
（
）.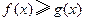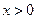