(本题10分)如图,以点M(-1,0)为圆心的圆与y轴、x轴分别交于点A、B、C、D,直线y=- x- 与⊙ M相切于点H,交x轴于点E,交y轴于点F.
M相切于点H,交x轴于点E,交y轴于点F.(1)请
 直接写出OE、⊙M的半径r、CH的长;
直接写出OE、⊙M的半径r、CH的长;(2)如图1,弦HQ交x轴于点P,且DP:PH=3:2,求COS∠QHC的值;
(3)如
 图2,点K为线段EC上一动点(不与E、C重合),连接BK交⊙M于点T,弦AT交x轴于点N.是否存在一个常数a,始终满足MN·MK=a,如果存在,请求出a的值;如果不存在,请说明理由.
图2,点K为线段EC上一动点(不与E、C重合),连接BK交⊙M于点T,弦AT交x轴于点N.是否存在一个常数a,始终满足MN·MK=a,如果存在,请求出a的值;如果不存在,请说明理由.
已知抛物线 的顶点为 ,与 轴的交点为 ,点 .
(Ⅰ) 求点 , 的坐标;
(Ⅱ) 将抛物线 向上平移得到抛物线 ,点 平移后的对应点为 ,且 .
①求抛物线 的解析式;
②若点 关于直线 的对称点为 ,射线 与抛物线 相交于点 ,求点 的坐标 .
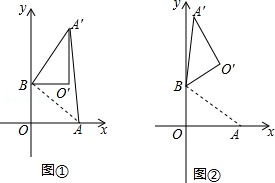
在平面直角坐标系中, 为原点,点 ,点 ,把 绕点 逆时针旋转,得△ ,点 , 旋转后的对应点为 , ,记旋转角为 .
(Ⅰ)如图①,若 ,求 的长;
(Ⅱ)如图②,若 ,求点 的坐标;
(Ⅲ)在(Ⅱ)的条件下,边 上 的一点 旋转后的对应点为 ,当 取得最小值时,求点 的坐标(直接写出结果即可)
公司有330台机器需要一次性运送到某地,计划租用甲、乙两种货车共8辆,已知每辆甲种货车一次最多运送机器45台、租车费用为400元,每辆乙种货车一次最多运送机器30台、租车费用为280元
(Ⅰ)设租用甲种货车 辆 为非负整数),试填写表格.
表一:
|
租用甲种货车的数量 辆 |
3 |
7 |
|
|
租用的甲种货车最多运送机器的数量 台 |
135 |
|
|
|
租用的乙种货车最多运送机器的数量 台 |
150 |
|
|
表二:
|
租用甲种货车的数量 辆 |
3 |
7 |
|
|
租用甲种货车的费用 元 |
|
2800 |
|
|
租用乙种货车的费用 元 |
|
280 |
|
(Ⅱ)给出能完成此项运送任务的最节省费用的租车方案,并说明理由.
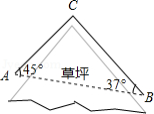
小明上学途中要经过 , 两地,由于 , 两地之间有一片草坪,所以需要走路线 , ,如图,在 中, , , ,求 , 的长.(结果保留小数点后一位)
参考数据: , , , 取1.414.
在 中, 为直径, 为 上一点.
(Ⅰ)如图1.过点 作 的切线,与 的延长线相交于点 ,若 ,求 的大小;
(Ⅱ)如图2, 为 上一点,且 经过 的中点 ,连接 并延长,与 的延长线相交于点 ,若 ,求 的大小.
