探索规律:观察下面由※组成的图案和算式,并解答问题
(
 )试猜想
)试猜想 ;
;(
 )试猜想
)试猜想 = ;
= ; (
 )请用上述规律计算:
)请用上述规律计算: (请算出最后数值哦!)
(请算出最后数值哦!)
2015年安徽省中考体育考试方案出台,体育总分由2014年的40分增加到45分,考试项目分为必考项目和选考项目.男生的必考项目是1000米跑,女生的必考项目是800米跑;选考项目为立定跳远、1分钟跳绳和坐位体前屈.某校为了解毕业班学生对选考项目的喜爱程度,以便进行有针对性的训练,对本校九年级部分学生进行了一次随机问卷调查,下图是采集数据后绘制的两幅不完整的统计图(A:立定跳远,B:1分钟跳绳,C:坐位体前屈).请你根据图中提供的信息解答以下问题:
(1)填写扇形统计图中缺失的数据,并把条形图补充完整;
(2)2015年该校九年级共有学生200人,按此调查,可以估计2015年该校九年级学生中喜爱1分钟跳绳的学生约有多少人?
(3)安徽省教育厅规定:各地市可在选考项目中确定两项作为本地市中考体育考试项目,那么该校所在地市确定的中考体育项目中“含有1分钟跳绳”的概率是多少?
如图,点D是等边△ABC中BC边上一点,过点D分别作DE∥AB,DF∥AC,交AC,AB于E,F,连接BE,CF,分别交DF,DE于点N,M,连接MN.试判断△DMN的形状,并说明理由.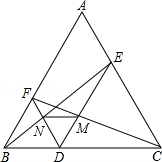
某商场销售国外、国内两种品牌的智能手机,这两种手机的进价和售价如下表所示:
| 国外品牌 |
国内品牌 |
|
| 进价(元/部) |
4400 |
2000 |
| 售价(元/部) |
5000 |
2500 |
该商场计划购进两种手机若干部,共需14.8万元,预计全部销售后可获毛利润共2.7万元.[毛利润=(售价﹣进价)×销售量]
(1)该商场计划购进国外品牌、国内品牌两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少国外品牌手机的购进数量,增加国内品牌手机的购进数量.已知国内品牌手机增加的数量是国外品牌手机减少的数量的3倍,而且用于购进这两种手机的总资金不超过15.6万元,该商场应该怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
某岛是我国南海上的一个岛屿,小明据此构造出该岛的一个数学模型如图甲所示,其中∠B=90°,AB=100 千米,∠BAC=30°,请据此解答如下问题:
千米,∠BAC=30°,请据此解答如下问题: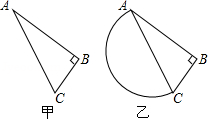
(1)求该岛的周长和面积(结果保留整数,参考数据 ≈1.414,
≈1.414, ≈1.73,
≈1.73, ≈2.45);
≈2.45);
(2)国家为了建设的需要,在原有岛屿基础上沿海岸线AC向海洋填海,扩充岛屿的面积(如图乙),填成一个以AC为直径的半圆,点D在这个半圆上,求当△ACD的面积最大时,△ACD另外两条边的边长.
如图所示,折线AOB可以看成是函数y=|x|(﹣1≤x≤1)的图象.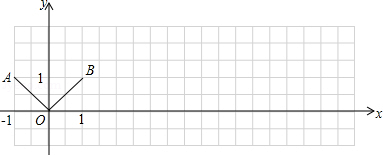
(1)将折线AOB向右平移4个单位,得到折线A1O1B1,画出折线A1O1B1;
(2)直接写出折线A1O1B1的表达式.