如图，在直角坐标系
中有一直角梯形
，
的中点为
，
，
，
，
，
，以
为焦点的椭圆经过点
.
（1）求椭圆的标准方程；
（2）若点
，问是否存在直线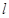
与椭圆交于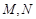
两点且
，若存在，求出直线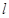的斜率的取值范围；若不存在，请说明理由.
已知二次函数f（x）的最小值为1,且f（0）=f（2）=3．
（1）求f（x）的解析式．
（2）若f（x）在区间[2a,a+1]上不单调,求实数a的取值范围．
（3）在区间[-1,1]上,y=f（x）的图象恒在y=2x+2m+1的图象上方,试确定实数m的取值范围．
已知函数f（x）= 
（1）判断函数在区间[1,+∞）上的单调性,并用定义证明你的结论．
（2）求该函数在区间[1,4]上的最大值与最小值．
已知函数f（x-1）=x2-4x,求函数f（x）,f（2x+1）的解析式．
若集合A＝{x|x2＋x－6＝0}，B＝{x|x2＋x＋a＝0}，且B⊆A，求实数a的取值范围．
已知集合A＝{x|3≤x<10}，集合B＝{x|2x－8≥0}．
（1）求A∪B；
（2）求∁R（A∩B）．