已知函数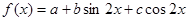 ;
; 的图像经过点
的图像经过点 ,且
,且 时,
时, 有最大值
有最大值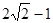 。
。
(1)求 的解析式;
的解析式;
(2) 能否通过平移变换,使得
能否通过平移变换,使得 的图像关于原点对称,如果能,请写出这个变换,如果不能,试说明理由
的图像关于原点对称,如果能,请写出这个变换,如果不能,试说明理由
如图,椭圆 的离心率为
的离心率为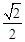 ,
, 轴被曲线
轴被曲线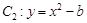 截得的线段长等于
截得的线段长等于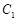 的短轴长。
的短轴长。 与
与 轴的交点为
轴的交点为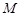 ,过坐标原点
,过坐标原点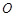 的直线
的直线 与
与 相交于点
相交于点 ,直线
,直线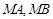 分别与
分别与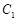 相交于点
相交于点 。
。
(1)求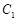 、
、 的方程;
的方程;
(2)求证: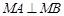 。
。
(3)记 的面积分别为
的面积分别为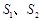 ,若
,若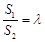 ,求
,求 的取值范围。
的取值范围。
已知数列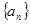 是等差数列,
是等差数列,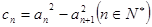
(1)判断数列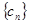 是否是等差数列,并说明理由;
是否是等差数列,并说明理由;
(2)如果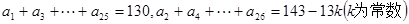 ,试写出数列
,试写出数列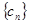 的通项公式;
的通项公式;
(3)在(2)的条件下,若数列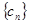 得前n项和为
得前n项和为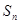 ,问是否存在这样的实数
,问是否存在这样的实数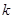 ,使
,使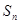 当且仅当
当且仅当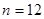 时取得最大值。若存在,求出
时取得最大值。若存在,求出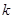 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
已知向量 记
记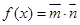 .
.
(1)若 ,求
,求 的值;
的值;
(2)在△ABC中,角A、B、C的对边分别是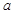 、
、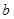 、
、 ,且满足
,且满足 ,若
,若 ,试判断△ABC的形状.
,试判断△ABC的形状.
已知曲线C上的动点P( )满足到定点A(-1,0)的距离与到定点B(1,0)距离之比为
)满足到定点A(-1,0)的距离与到定点B(1,0)距离之比为
(1)求曲线C的方程。
(2)过点M(1,2)的直线 与曲线C交于两点M、N,若|MN|=4,求直线
与曲线C交于两点M、N,若|MN|=4,求直线 的方程。
的方程。