(本小题满分14分)
已知函数f(x)=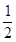 x
x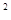 -ax + (a-1)
-ax + (a-1)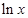 ,
,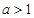 .
.
(I)讨论函数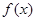 的单调性;
的单调性;
(II)若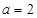 ,数列
,数列 满足
满足 .
.
(1) 若首项 ,证明数列
,证明数列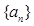 为递增数列;
为递增数列;
(2) 若首项为正整数,数列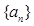 递增,求首项的最小值.
递增,求首项的最小值.
(本小题满分10分)在甲、乙两个盒子中分别装有标号为1,2,3,4的四个球,现从甲、乙两个盒子中各取出1个球,每个球被取出的可能性相等.
(1)求取出的两个球上标号为相同数字的概率;
(2)求取出的两个球上标号之积能被3整除的概率.
(本小题满分10分)从甲、乙两名学生中选拔一人参加射箭比赛,为此需要对他们的射箭水平进行测试.现这两名学生在相同条件下各射箭10次,命中的环数如下:
| 甲 |
8 |
9 |
7 |
9 |
7 |
6 |
10 |
10 |
8 |
6 |
| 乙 |
10 |
9 |
8 |
6 |
8 |
7 |
9 |
7 |
8 |
8 |
(1)计算甲、乙两人射箭命中环数的平均数和标准差;
(2)比较两个人的成绩,然后决定选择哪名学生参加射箭比赛.
(本小题满分10分)经过点P(3,2)的一条动直线分别交x轴、y轴于点A、B,M是线段AB的中点,连结OM并延长至点N,使|ON|=2|OM|,求点N的轨迹方程.
已知函数 是定义在
是定义在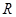 上的偶函数,当
上的偶函数,当 时,
时, 。
。
(1)求 的函数解析式,并用分段函数的形式给出;
的函数解析式,并用分段函数的形式给出;
(2)作出函数 的简图;
的简图;
(3)写出函数 的单调区间及最值.
的单调区间及最值.
(本题16分)某公司生产一种电子仪器的固定成本为20 000元,每生产一台仪器需增加投入100元,已知总收益满足函数: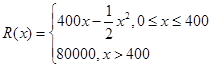 (其中x是仪器的月产量).
(其中x是仪器的月产量).
(1)将利润表示为月产量的函数f(x);
(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?(总收益=总成本+利润)