已知函数 。
。
(1)判断函数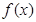 在区间
在区间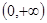 上的单调性并证明;
上的单调性并证明;
(2)求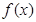 在区间
在区间 上的最大值和最小值。
上的最大值和最小值。
在平面直角坐标系xOy中,曲线y=x2-6x+1与坐标轴的交点都在圆C上.
(1)求圆C的方程;
(2)若圆C与直线x-y+a=0交于A,B两点,且OA⊥OB,求a的值.
如图,在四棱锥 中,底面
中,底面 是正方形,侧面
是正方形,侧面
 底面
底面 ,且
,且 ,
, 、
、 分别为
分别为 、
、 的中点.
的中点.
(Ⅰ)求证:直线 ∥平面
∥平面 ;
;
(Ⅱ)求证:直线
 平面
平面 .
.
已知以点C为圆心的圆经过点A(3,1)和B(1,3),且圆自身关于直线 对称.设直线
对称.设直线 :
: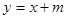 .
.
(1)求圆C的方程;
(2)在圆C上,若到直线 :
: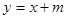 的距离等于1的点恰有4个,求
的距离等于1的点恰有4个,求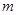 的取值范围.
的取值范围.
如图,矩形ABCD的两条对角线相交于点M(3,5),AB边所在直线的方程为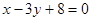 ,点N(0,6)在AD边所在直线上.
,点N(0,6)在AD边所在直线上.
(1)求AD边所在直线的方程;
(2)求对角线AC所在直线的方程.
已知圆 :
: ,点
,点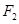 (1, 0),点
(1, 0),点 在圆
在圆 上运动,
上运动,  的垂直平分线交
的垂直平分线交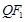 于点
于点 .
.
(1) 求动点 的轨迹
的轨迹 的方程;
的方程;
(2)设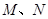 分别是曲线
分别是曲线 上的两个不同点,且点
上的两个不同点,且点 在第一象限,点
在第一象限,点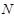 在第三象限,若
在第三象限,若 ,
, 为坐标原点,求直线
为坐标原点,求直线 的斜率;
的斜率;
(3)过点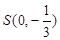 的动直线
的动直线 交曲线
交曲线 于
于 两点,求证:以
两点,求证:以 为直径的圆恒过定点
为直径的圆恒过定点