已知集合U={x|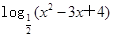 >-2且x∈Z},集合A={x|ax-1=0},集合B={x|
>-2且x∈Z},集合A={x|ax-1=0},集合B={x|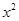 -(a+3)x+2a+2=0),若CUA=B,求a的值.
-(a+3)x+2a+2=0),若CUA=B,求a的值.
在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2, ,6)的同学所得成绩,且前5位同学的成绩如下:
| 编号n |
1 |
2 |
3 |
4 |
5 |
| 成绩xn |
70 |
76 |
72 |
70 |
72 |
(1)求第6位同学的成绩x6,及这6位同学成绩的标准差s;
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
△ABC的三个内角A、B、C所对边长分别为a、b、c,已知c=3,C=60°。
(1)若A=75°,求b的值;(2)若a=2 b, 求b的值。
已知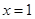 是函数
是函数 的一个极值点,其中
的一个极值点,其中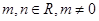
(1)求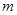 与
与 的关系式;
的关系式;
(2)求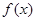 的单调区间;
的单调区间;
(3)设函数函数g(x)= 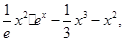
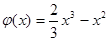 ;试比较g(x)与
;试比较g(x)与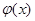 的大小。
的大小。
设函数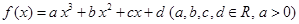 , 其中
, 其中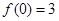 ,
, 是
是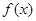 的导函数.
的导函数.
(Ⅰ)若 ,求函数
,求函数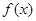 的解析式;
的解析式;
(Ⅱ)若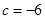 ,函数
,函数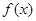 的两个极值点为
的两个极值点为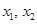 满足
满足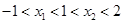 . 设
. 设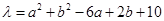 , 试求实数
, 试求实数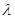 的取值范围.
的取值范围.
已知函数 .
.
(Ⅰ)求 的最小值;
的最小值;
(Ⅱ)若对所有 都有
都有 ,求实数
,求实数 的取值范围.
的取值范围.