(本题满分7分)
已知直线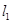 :
: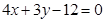 与
与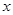 轴和
轴和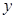 轴分别交于
轴分别交于 两点,直线
两点,直线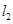 经过点
经过点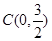 且与直线
且与直线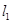 垂直,垂足为
垂直,垂足为 .
.
(Ⅰ)求直线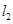 的方程与点
的方程与点 的坐标;
的坐标;
(Ⅱ)若将四边形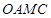 (
(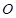 为坐标原点)绕
为坐标原点)绕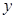 轴旋转一周得到一几何体,求该几何体的体积
轴旋转一周得到一几何体,求该几何体的体积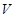 .
.
(Ⅰ)设函数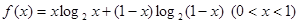 ,求
,求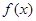 的最小值;
的最小值;
(Ⅱ)设正数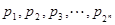 满足
满足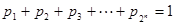 ,证明
,证明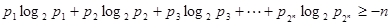
甲、乙等五名志愿者被随机地分到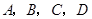 四个不同的岗位服务,每个岗位至少有一名志愿者.
四个不同的岗位服务,每个岗位至少有一名志愿者.
(Ⅰ)求甲、乙两人同时参加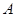 岗位服务的概率;
岗位服务的概率;
(Ⅱ)设随机变量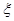 为这五名志愿者中参加
为这五名志愿者中参加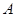 岗位服务的人数,求
岗位服务的人数,求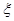 的分布列.
的分布列.
已知圆C的极坐标方程是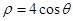 ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线
,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线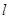 的参数方程是
的参数方程是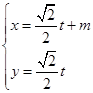 (t是参数)。若直线
(t是参数)。若直线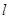 与圆C相切,求实数m的值。
与圆C相切,求实数m的值。
将曲线 绕坐标原点按逆时针方向旋转45°,求所得曲线的方程.
绕坐标原点按逆时针方向旋转45°,求所得曲线的方程.
(本题满分16分)对于数列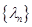 ,若存在常数M>0,对任意
,若存在常数M>0,对任意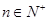 ,恒有
,恒有
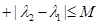 ,则称数列
,则称数列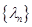 为
为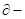 数列.
数列.
求证:⑴设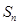 是数列
是数列 的前n项和,若
的前n项和,若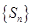 是
是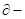 数列,则
数列,则 也是
也是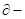 数列.
数列.
⑵若数列 都是
都是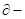 数列,则
数列,则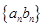 也是
也是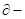 数列.
数列.