在两个袋子中分别装有大小、质地完全相同的的卡片. 甲袋中放了３张卡片，卡片上的数字分别为1，2，3；乙袋中放了2张卡片，卡片上的数字分别为4，5．张红和李欣两人做游戏，分别从甲、乙两个袋子中随机地各摸出一张卡片，若所摸出的两张卡片上的数字之和为奇数，则判张红获胜；若两张卡片上的数字之和
为偶数，则判李欣获胜．你认为这个游戏公平吗？请写出你的判断，并用列表或画树状图的方法加以说明．
在△ABC中，BE、CF分别是AC、AB两条边上的高，在BE上截取BD＝AC，在CF的延长线上截取CG＝AB，连结AD、AG。求证：AG＝AD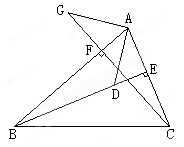
如图，点D，E分别在AC，AB上．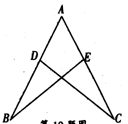
(1) 已知，BD=CE，CD=BE，求证：AB=AC；
(2) 分别将“BD=CE”记为①，“CD=BE” 记为②，“AB=AC”记为③．添加条件①、③，以②为结论构成命题1，添加条件②、③以①为结论构成命题2．命题1是命题2的命题，命题2是
命题．（选择“真”或“假”填入空格）．
已知：△ABC≌△A′B′C′，AD、A′D′分别是对应边BC和B′C′边上的高。
求证：AD=A′D′。
如图，点A、F、C、D在同一直线上，点B和点E分别在直线AD的两侧，且AB＝DE，∠A＝∠D，AF＝DC．
求证：BC∥EF．
已知：如图，四边形ABCD中，AB∥CD ，AD∥BC。
求证：△ABD≌△CDB。