已知在直角坐标平面XOY中,有一个不在Y轴上的动点P(x,y),到定点F(0, )的距离比它到X轴的距离多
)的距离比它到X轴的距离多 ,记P点的轨迹为曲线C
,记P点的轨迹为曲线C
(I)求曲线C的方程;
(II)已知点M在Y轴上,且过点F的直线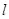 与曲线C交于A、B两点,若
与曲线C交于A、B两点,若  为正三角形,求M点的坐标与直线
为正三角形,求M点的坐标与直线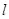 的方程。
的方程。
(本小题满分12分)
某服装商场为了了解毛衣的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
(1) 算出线性回归方程 ;(a,b精确到十分位)
;(a,b精确到十分位)
(2)气象部门预测下个月的平均气温约为6℃,据此估计,求该商场下个月毛衣的销售量.
(本小题满分12分)
在三棱柱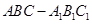 中,侧棱
中,侧棱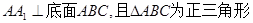 ,点
,点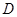 是
是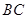 的中点,
的中点,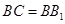 .
.
(1)求证: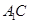 ∥平面
∥平面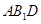 ;
;
(2) 为棱
为棱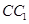 的中点,试证明:
的中点,试证明: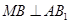 .
.
(本小题满分12分)
编写一个算法流程图,对于函数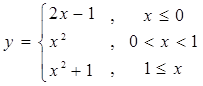 输入x的值,输出相应的函数值,并用基本语句表示此算法。
输入x的值,输出相应的函数值,并用基本语句表示此算法。
(本小题满分12分)某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如右图所示.
(1)下表是年龄的频数分布表,求正整数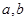 的值;
的值;
| 区间 |
[25,30) |
[30,35) |
[35,40) |
[40,45) |
[45,50] |
| 人数 |
50 |
50 |
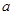 |
150 |
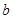 |
(2)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,年龄在第1,2,3组的人数分别是多少?
(3)在(2)的前提下,从这6人中随机抽取2人参加社区宣传交流活动,求至少有1人年龄在第3组的概率.
(不计入总分):已知函数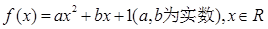 ,设函数
,设函数 ,
,
(3)当a≠0时,求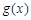 在
在 上的最小值
上的最小值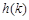 .
.