如图,已知椭圆 的离心率为
的离心率为 ,以该椭圆上的点和椭圆的左、右焦点
,以该椭圆上的点和椭圆的左、右焦点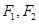 为顶点的三角形的周长为
为顶点的三角形的周长为 .一等轴双曲线的顶点是该椭圆的焦点,设
.一等轴双曲线的顶点是该椭圆的焦点,设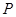 为该双曲线上异于顶点的任一点,直线
为该双曲线上异于顶点的任一点,直线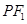 和
和 与椭圆的交点分别为
与椭圆的交点分别为 和
和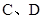 .
.
(Ⅰ)求椭圆和双曲线的标准方程;
(Ⅱ)设直线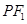 、
、 的斜率分别为
的斜率分别为 、
、 ,证明
,证明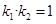 ;
;
(Ⅲ)是否存在常数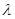 ,使得
,使得 恒成立?若
恒成立?若 存在,求
存在,求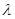 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.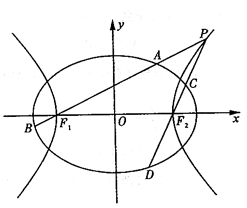
选修4-4:坐标系与参数方程选讲
在直角坐标系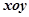 中,曲线
中,曲线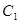 的参数方程为
的参数方程为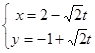 (
( 为参数),以原点为极点,以
为参数),以原点为极点,以 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线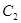 的极坐标方程为
的极坐标方程为
(1)求曲线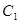 的普通方程与曲线
的普通方程与曲线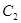 的直角坐标方程;
的直角坐标方程;
(2)设点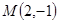 ,曲线
,曲线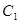 与曲线
与曲线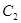 交于
交于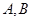 ,求
,求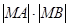 的值.
的值.
选修4-1:几何证明选讲.
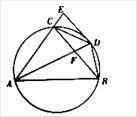
如图,圆周角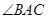 的平分线与圆交于点
的平分线与圆交于点 ,过点
,过点 的切线与弦
的切线与弦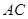 的延长线交于点
的延长线交于点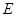 ,
, 交
交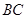 于点
于点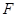 .
.
(1)求证: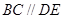 ;
;
(2)若 四点共圆,且弧
四点共圆,且弧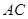 与弧
与弧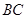 相等,求
相等,求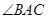
设函数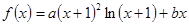 ,其中
,其中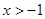 ,曲线
,曲线 过点
过点 ,且在点
,且在点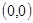 处的切线方程为
处的切线方程为 .
.
(1)求 的值;
的值;
(2)证明:当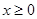 时,
时,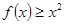 ;
;
(3)若当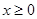 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知抛物线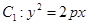 上一点
上一点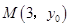 到其焦点
到其焦点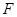 的距离为4;椭圆
的距离为4;椭圆 的离心率
的离心率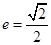 ,且过抛物线的焦点
,且过抛物线的焦点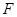 .
.
(1)求抛物线 和椭圆
和椭圆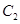 的标准方程;
的标准方程;
(2)过点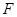 的直线
的直线 交抛物线
交抛物线 于
于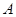 、
、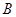 两不同点,交
两不同点,交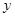 轴于点
轴于点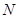 ,已知
,已知 ,求证:
,求证: 为定值.
为定值.
(3)直线 交椭圆
交椭圆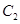 于
于 ,
, 两不同点,
两不同点, ,
, 在
在 轴的射影分别为
轴的射影分别为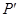 ,
,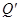 ,
, ,若点S满足:
,若点S满足: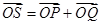 ,证明:点S在椭圆
,证明:点S在椭圆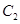 上.
上.
某中学举行了一次“环保知识竞赛”活动.为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计.按照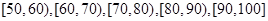 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在 的数据).
的数据).
(Ⅰ)求样本容量n和频率分布直方图中x、y的值;
(Ⅱ)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取3名同学到市政广场参加环保知识宣传的志愿者活动,设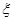 表示所抽取的3名同学中得分在
表示所抽取的3名同学中得分在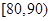 的学生个数,求
的学生个数,求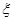 的分布列及其数学期望.
的分布列及其数学期望.