定义：如果数列
的任意连续三项均能构成一个三角形的三边长，则称为“三角形”数列．对于“三角形”数
列，如果函数
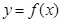使得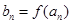
仍为一个“三角形”数列，则称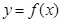是数列的“保三角形函数”，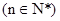
.
（Ⅰ）已知
是首项为2，公差为1的等差数列，若
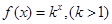是数列的“保三角形函数”，求k的取值范围；
（Ⅱ）已知数列
的首项为2010，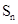
是数列的前n项和，且满足
，证明是“三角形”数列；
（Ⅲ）根据“保三角形函数”的定义，对函数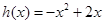
，
，和数列1，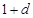
，
，（
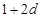）提出一个正确的命题，并说明理由．
已知f(x)是R上的奇函数，且当x∈(-∞,0)时，f(x)=-xlg(2-x),求f(x)的解析式.
已知f(x)是实数集R上的函数，且对任意x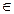
R,f(x)=f(x+1)+f(x-1)恒成立.
(1)求证：f(x)是周期函数.
(2)已知f(3)=2，求f(2 004).
设f（x）是定义在R上的偶函数，其图象关于直线x=1对称，对任意x1、x2∈［0，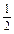
］都有f（x1+x2）=f（x1）·f（x2），且f(1)=a＞0.
（1）求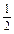f()及f(
)
（2）证明：f（x）是周期函数；
（3）记an=f(2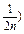n+
，求an.
已知函数y=f(x)的定义域为R，且对任意a,b∈R,都有f(a+b)=f(a)+f(b)，且当x＞0时，f(x)＜0恒成立，f(3)="-3."
(1)证明：函数y=f(x)是R上的减函数；
（2）证明：函数y=f(x)是奇函数；
（3）试求函数y=f(x)在［m,n］（m,n∈Z）上的值域.
判断下列各函数的奇偶性：
（1）f（x）=（x-2）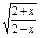
；
（2）f（x）=
；
（3）f（x）=