(本小题满分12分）
已知公比大于1的等比数列{
}满足：
+
+
=28，且+2是和的等差中项.
（Ⅰ）求数列{}的通项公式；
（Ⅱ）若
=
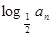，求{}的前n项和
.
已知椭圆C：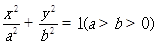
的离心率为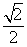
，其中左焦点
．
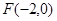（Ⅰ）求出椭圆C的方程；
（Ⅱ） 若直线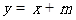
与曲线C交于不同的A、B两点，且线段AB的中点M在圆
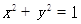上，求m的值．
在如图所示的多面体ABCDE中，AB⊥平面ACD，DE⊥平面ACD，
且AC=AD=CD=DE=2，AB=1．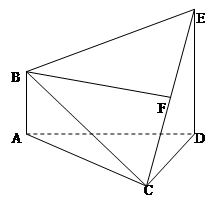
（Ⅰ）请在线段CE上找到点F的位置，使得恰有直线BF∥平面ACD，并证明这一事实；
（Ⅱ）求多面体ABCDE的体积．
已知函数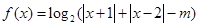
．
（Ⅰ）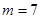
时，求函数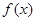
的定义域；
（Ⅱ）若关于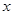
的不等式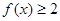
的解集是R，求
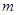的取值范围．
在△ABC中，角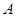
、
、
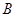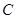所对的边分别为
、
、
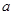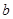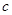，已知向量
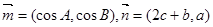，且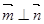
．
（Ⅰ） 求角A的大小；
（Ⅱ） 若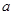
，
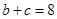，求△ABC的面积．
已知点
，参数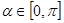
，点Q在曲线C：
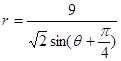上．
（Ⅰ）求点P的轨迹方程与曲线C的直角坐标方程；
（Ⅱ）求点P与点Q之间的最小值．