已知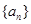 是公差不为零的等差数列,
是公差不为零的等差数列, ,且
,且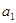 ,
,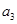 ,
, 成等比数列.
成等比数列.
(I)求数列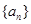 的通项;
的通项;
(II)记 ,数列
,数列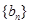 的前
的前 项和为
项和为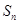 .求证
.求证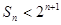
(本小题满分10分)(Ⅰ)求以下不等式的解集:
(1) (2)
(2)
(Ⅱ)若关于x的不等式 的解集为
的解集为 ,求实数m的值.
,求实数m的值.
(满分14分) 已知:定义在R上的函数 ,对于任意实数a, b都满足
,对于任意实数a, b都满足 ,且
,且 ,当
,当 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)证明 在
在 上是增函数;
上是增函数;
(Ⅲ)求不等式 的解集.
的解集.
(满分14分)已知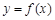 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当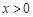 时,
时, .
.
(Ⅰ)求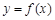 的解析式;
的解析式;
(Ⅱ)问是否存在这样的正数a, b使得当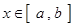 时,函数
时,函数 的值域为
的值域为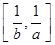 ,若存在,求出所有a, b的值,若不存在,说明理由.
,若存在,求出所有a, b的值,若不存在,说明理由.
(满分14分)已知函数 (a为常数)是奇函数.
(a为常数)是奇函数.
(Ⅰ)求a的值与函数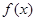 的定义域;
的定义域;
(Ⅱ)若当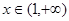 时,
时,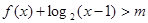 恒成立.求实数
恒成立.求实数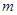 的取值范围.
的取值范围.
(满分14分)已知集合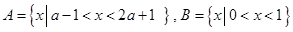 .
.
(Ⅰ)若 ;
;
(Ⅱ)若 ,求实数a.
,求实数a.