已知函数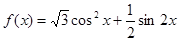 .
.
(Ⅰ)求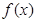 的最小正周期;
的最小正周期;
(Ⅱ)求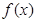 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
已知动点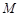 到定点
到定点 的距离比到直线
的距离比到直线 的距离小1.
的距离小1.
(1)求动点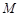 的轨迹
的轨迹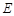 的方程;
的方程;
(2)取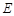 上一点
上一点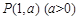 ,任作弦
,任作弦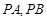 ,满足
,满足 ,则弦
,则弦 是否经过一个定点?若经过定点(设为点
是否经过一个定点?若经过定点(设为点 ),请写出
),请写出 点的坐标,否则说明理由.
点的坐标,否则说明理由.
已知函数 .
.
(1)求函数 的极大值;
的极大值;
(2)若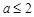 时,存在
时,存在 的图象在
的图象在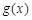 图象的上方,求实数
图象的上方,求实数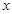 的取值范围.
的取值范围.
已知三棱锥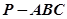 中,
中, ,
, ,
,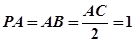 ,
,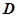 ,
,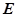 分别是
分别是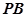 ,
,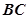 中点.
中点.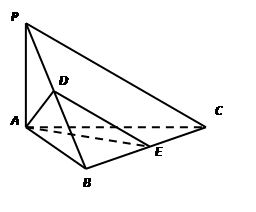
(1)求证: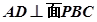 ;
;
(2)求直线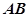 与平面
与平面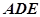 所成角的正弦值.
所成角的正弦值.
设公比大于零的等比数列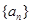 的前
的前 项和为
项和为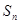 ,且
,且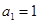 ,[
,[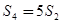 ,数列
,数列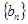 的前
的前 项和为
项和为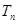 ,满足
,满足 ,
,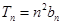 ,
,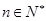 .
.
(1)求数列 、
、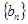 的通项公式;
的通项公式;
(2)满足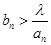 对所有的
对所有的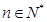 均成立,求实数
均成立,求实数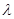 的取值范围.
的取值范围.
△ABC的内角A,B,C对边分别是a,b,c,且 ,
,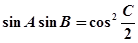 .
.
(1)求角A与角B的大小;
(2)若BC边上的中线AM的长为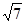 ,求△ABC的面积.
,求△ABC的面积.