△ABC的内角A,B,C对边分别是a,b,c,且 ,
,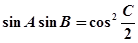 .
.
(1)求角A与角B的大小;
(2)若BC边上的中线AM的长为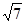 ,求△ABC的面积.
,求△ABC的面积.
(1)解关于x的不等式
(2)记a>0时(1)中不等式的解集为A,集合B= ,若
,若 恰有3个元素,求a的取值范围。
恰有3个元素,求a的取值范围。
设 ,
,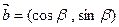
(1)若 ,
, 为
为 与
与 的夹角,求
的夹角,求 。
。
(2)若 与
与 夹角为60o,那么t为何值时
夹角为60o,那么t为何值时 的值最小?
的值最小?
(本小题满分14分)已知抛物线 ,椭圆经过点
,椭圆经过点 ,它们在
,它们在 轴上有共同焦点,椭圆的对称轴是坐标轴.(Ⅰ)求椭圆的方程;(Ⅱ)若
轴上有共同焦点,椭圆的对称轴是坐标轴.(Ⅰ)求椭圆的方程;(Ⅱ)若 是椭圆上的点,设
是椭圆上的点,设 的坐标为
的坐标为 (
(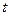 是已知正实数),求
是已知正实数),求 与
与 之间的最短距离.
之间的最短距离.
(本小题满分14分)甲、乙两间商店购进同一种商品的价格均为每件30元,销售价均为每件50元.根据前5年的有关资料统计,甲商店这种商品的年需求量 服从以下分布:
服从以下分布:
 |
10 |
20 |
30 |
40 |
50 |
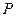 |
0.15 |
0.20 |
0.25 |
0.30 |
0.10 |
乙商店这种商品的年需求量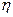 服从二项分布
服从二项分布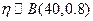 .
.
若这种商品在一年内没有售完,则甲商店在一年后以每件25元的价格处理;乙商店一年后剩下的这种商品第1件按25元的价格处理,第2件按24元的价格处理,第3件按23元的价格处理,依此类推.今年甲、乙两间商店同时购进这种商品40件,根据前5年的销售情况,请你预测哪间商店的期望利润较大?
(本小题满分14分)如图某一几何体的展开图,其中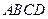 是边长为6的正方形,
是边长为6的正方形,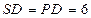 ,
,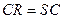 ,
,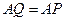 ,点
,点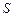 、
、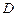 、
、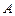 、
、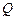 及
及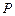 、
、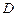 、
、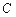 、
、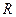 共线.(Ⅰ)沿图中虚线将它们折叠起来,使
共线.(Ⅰ)沿图中虚线将它们折叠起来,使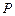 、
、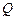 、
、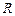 、
、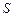 四点重合为点
四点重合为点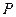 ,请画出其直观图;
,请画出其直观图;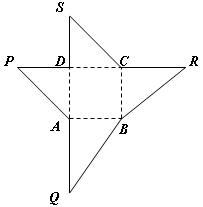

(Ⅱ)求二面角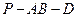 的大小;(Ⅲ)试问需要几个这样的几何体才能拼成一个棱长为6的正方体
的大小;(Ⅲ)试问需要几个这样的几何体才能拼成一个棱长为6的正方体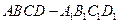 ?
?