一个盒子中装有4张卡片,每张卡片上写有1个数字,数字分别是1、2、3、4,现从盒子中随机抽取卡片.
(1)若一次从中随机抽取3张卡片,求3张卡片上数字之和大于或等于7的概率;
(2)若第一次随机抽1张卡片,放回后再随机抽取1张卡片,求两次抽取中至少一次抽到
数字2的概率
(本小题满分12分)已知椭圆的一个顶点为 ,焦点在
,焦点在 轴上.若右焦点到直线
轴上.若右焦点到直线 的距离为3.
的距离为3.
(1)求椭圆的方程;
(2)设椭圆与直线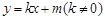 相交于不同的两点
相交于不同的两点 .当
.当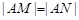 时,求
时,求 的取值范围.
的取值范围.
(本小题满分12分)已知数列 的各项均为正数,观察程序框图,若
的各项均为正数,观察程序框图,若 时,分别有
时,分别有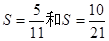 .
.
(1)试求数列 的通项公式;
的通项公式;
(2)令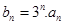 ,求数列
,求数列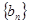 的前
的前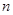 项和
项和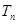 .
.
(本小题满分12分)如图,直三棱柱 中,
中, 分别是
分别是 ,
, 的中点。
的中点。
(1)证明: 平面
平面 ;
;
(2)设 ,求异面直线
,求异面直线 与
与 所成角的大小.
所成角的大小.
(本小题满分12分)已知 ,
, ,
,
且函数
(1)设方程 在
在 内有两个零点
内有两个零点 ,求
,求 的值;
的值;
(2)若把函数 的图像向左平移
的图像向左平移 个单位,再向上平移2个单位,得函数
个单位,再向上平移2个单位,得函数 图像,求函数
图像,求函数 在
在 上的单调增区间.
上的单调增区间.
(本小题满分10分)已知幂函数 在
在 上单调递增,函数
上单调递增,函数
(1)求 的值;
的值;
(2)当 时,记
时,记 的值域分别为
的值域分别为 ,若
,若 ,求实数
,求实数 的取值范围.
的取值范围.