(本小题满分14分)
已知函数 .
.
(I)当 时,求函数
时,求函数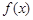 的单调区间;
的单调区间;
(II)若函数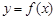 的图象在点
的图象在点 处的切线的倾斜角为45o,问:m在什么范围取值时,对于任意的
处的切线的倾斜角为45o,问:m在什么范围取值时,对于任意的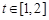 ,函数
,函数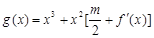 在区间
在区间 上总存在极值?
上总存在极值?
某一中学生心理咨询中心服务电话接通率为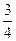 ,某班3名同学商定明天分别就同一问题询问该服务中心.且每人只拨打一次,求他们中成功咨询的人数
,某班3名同学商定明天分别就同一问题询问该服务中心.且每人只拨打一次,求他们中成功咨询的人数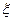 的分布列.
的分布列.
某射手有5发子弹,射击一次命中概率为0.9,如果命中就停止射击,否则一直到子弹用尽,求耗用子弹数 的分布列.
的分布列.
一批产品共100件,其中有10件是次品,为了检验其质量,从中以随机的方…式选取5件,求在抽取的这5件产品中次品数分布列与期望值,并说明5件中有3件以上(包括3件)为次品的概率.(精确到0.001)
某批数量较大的商品的次品率是5%,从中任意地连续取出10件, 为所含次品的个数,求
为所含次品的个数,求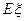 .
.
有n把看上去样子相同的钥匙,其中只有一把能把大门上的锁打开.用它们去试开门上的锁.设抽取钥匙是相互独立且等可能的.每把钥匙试开后不能放回.求试开次数 的数学期望和方差.
的数学期望和方差.