如图,在平面直角坐标系中,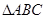 的顶点坐标为
的顶点坐标为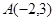 、
、 、
、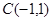
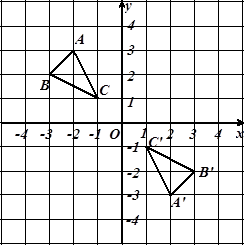
(1)若将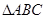 向右平移3个单位长度,再向上平移
向右平移3个单位长度,再向上平移 1个单位长度,请画出平移后的
1个单位长度,请画出平移后的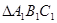 ;
;
(2)画出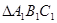 绕原点旋转
绕原点旋转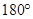 后得到的
后得到的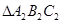 ;
; (3)
(3)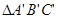 与
与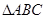 是位似图形,请写出位似中心的坐标: ;
是位似图形,请写出位似中心的坐标: ;
(4)顺次连结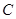 、
、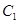 、
、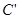 、
、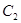 ,所得到的图形是轴对称图形吗?
,所得到的图形是轴对称图形吗?
答: (填“是”或“不是”).
如图①,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水, 时注满水槽.水槽内水面的高度 与注水时间 之间的函数图象如图②所示.
(1)正方体的棱长为 ;
(2)求线段 对应的函数解析式,并写出自变量 的取值范围;
(3)如果将正方体铁块取出,又经过 恰好将此水槽注满,直接写出 的值.

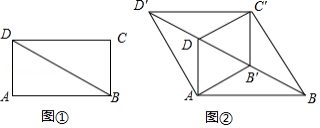
如图①, 是矩形 的对角线, , .将 沿射线 方向平移到△ 的位置,使 为 中点,连接 , , , ,如图②.
(1)求证:四边形 是菱形;
(2)四边形 的周长为 ;
(3)将四边形 沿它的两条对角线剪开,用得到的四个三角形拼成与其面积相等的矩形,直接写出所有可能拼成的矩形周长.
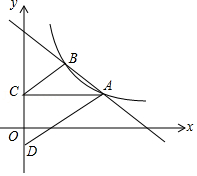
如图,在平面直角坐标系中,直线 与函数 的图象交于点 , .过点 作 平行于 轴交 轴于点 ,在 轴负半轴上取一点 ,使 ,且 的面积是6,连接 .
(1)求 , , 的值;
(2)求 的面积.
如图,一枚运载火箭从距雷达站 处 的地面 处发射,当火箭到达点 , 时,在雷达站 处测得点 , 的仰角分别为 , ,其中点 , , 在同一条直线上.求 , 两点间的距离(结果精确到 .
(参考数据: , , .

图①、图②、图③都是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点称为格点.线段 的端点在格点上.

(1)在图①、图2中,以 为边各画一个等腰三角形,且第三个顶点在格点上;(所画图形不全等)
(2)在图③中,以 为边画一个平行四边形,且另外两个顶点在格点上.