一个盒子装有六张卡片,上面分别写着如下六个函数: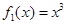 ,
, ,
,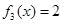 ,
, ,
, ,
, .
.
(Ⅰ)从中任意拿取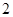 张卡片,若其中有一张卡片上写着的函数为奇函数。在此条件下,求两张卡片上写着的函数相加得到的新函数为奇函数的概率;
张卡片,若其中有一张卡片上写着的函数为奇函数。在此条件下,求两张卡片上写着的函数相加得到的新函数为奇函数的概率;
(Ⅱ)现从盒子中逐一抽取卡片,且每次取出后均不放回,若取到一张写有偶函数的卡片则停止抽取,否则继续进行,求抽取次数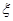 的分布列和数学期望.
的分布列和数学期望.
已知抛物线 :
: 的焦点为
的焦点为 ,抛物线上的点
,抛物线上的点 到焦点的距离为3,椭圆
到焦点的距离为3,椭圆 :
: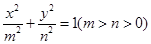 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,且离心率为
的焦点重合,且离心率为 .
.
(1)求抛物线 和椭圆
和椭圆 的方程;
的方程;
(2)已知直线 :
: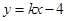 交椭圆
交椭圆 于
于 、
、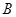 两个不同的点,若原点
两个不同的点,若原点 在以线段
在以线段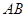 为直径的圆的外部,求
为直径的圆的外部,求 的取值范围.
的取值范围.
如图,在边长为4的菱形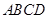 中,∠
中,∠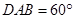 ,点
,点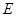 ,
,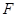 分别是边
分别是边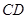 ,
,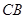 的中点,
的中点,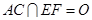 ,沿
,沿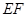 将△
将△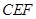 翻折到△
翻折到△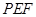 ,连接
,连接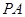 ,
,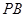 ,
,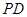 ,得到如图2的五棱锥
,得到如图2的五棱锥 ,且
,且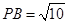 .
.
(1)求证: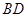 ⊥平面
⊥平面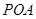
(2)求四棱锥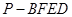 的体积.
的体积.
今年暑假期间,雅礼中学组织学生进社区开展社会实践活动.部分学生进行了关于“消防安全”的调查,随机抽取了50名居民进行问卷调查,活动结束后,对问卷结果进行了统计,并将其中“是否知道灭火器使用方法(知道或不知道)”的调查结果统计如下表:
| 年龄(岁) |
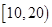 |
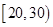 |
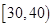 |
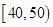 |
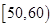 |
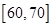 |
| 频数 |
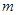 |
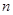 |
14 |
12 |
8 |
6 |
| 知道的人数 |
3 |
4 |
8 |
7 |
3 |
2 |
(1)求上表中的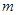 、
、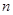 的值,并补全下图所示的频率分布直方图;
的值,并补全下图所示的频率分布直方图;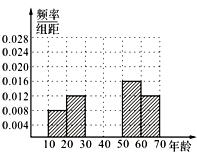
(2)在被调查的居民中,若从年龄在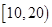 ,
,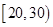 的居民中各随机选取1人参加消防知识讲座,求选中的两人中仅有一人不知道灭火器的使用方法的概率.
的居民中各随机选取1人参加消防知识讲座,求选中的两人中仅有一人不知道灭火器的使用方法的概率.
已知数列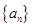 各项均为正,且
各项均为正,且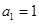 ,
,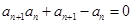 (
(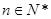 ).
).
(1)设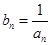 ,求证:数列
,求证:数列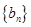 是等差数列;
是等差数列;
(2)求数列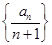 的前
的前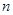 项和.
项和.
定义在 上的函数
上的函数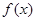 满足:对
满足:对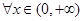 ,都有
,都有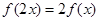 ;当
;当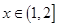 时,
时,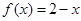 ,给出如下结论:其中所有正确结论的序号是: .
,给出如下结论:其中所有正确结论的序号是: .
①对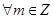 ,有
,有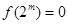 ;
;
②函数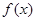 的值域为
的值域为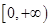 ;
;
③存在 ,使得
,使得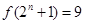 ;
;
④函数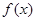 在区间
在区间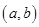 单调递减的充分条件是“存在
单调递减的充分条件是“存在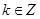 ,使得
,使得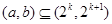 ”.
”.