已知m∈R,直线l:mx-(m2+1)y=4m和圆C:x2+y2-8x+4y+16=0.
(1)求直线l斜率的取值范围;
(2)直线l能否将圆C分割成弧长的比值为的两段圆弧?为什么?
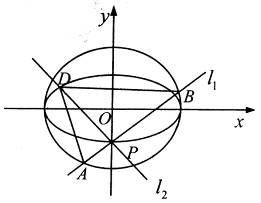
如图,点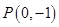 是椭圆
是椭圆 的一个顶点,
的一个顶点, 的长轴是圆
的长轴是圆 的直径,
的直径, 、
、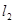 是过点
是过点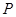 且互相垂直的两条直线,其中
且互相垂直的两条直线,其中 交圆
交圆 于
于 、
、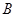 两点,
两点,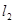 交椭圆
交椭圆 于另一点
于另一点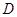 .
.
(1)求椭圆 的方程;
的方程;
(2)求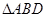 面积的最大值及取得最大值时直线
面积的最大值及取得最大值时直线 的方程.
的方程.
已知等差数列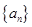 的首项
的首项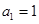 ,公差
,公差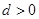 ,且
,且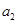 、
、 、
、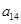 分别是等比数列
分别是等比数列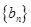 的
的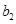 、
、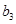 、
、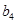 .
.
(1)求数列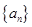 和
和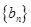 的通项公式;
的通项公式;
(2)设数列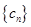 对任意正整数
对任意正整数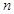 均有
均有 成立,求
成立,求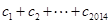 的值.
的值.
在如图所示的几何体中,四边形 为平行四边形,
为平行四边形, ,
,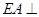 平面
平面 ,
,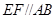 ,
, ,
, ,
,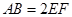 .
.
(1)若 是线段
是线段 的中点,求证:
的中点,求证: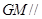 平面
平面 ;
;
(2)若 ,求二面角
,求二面角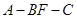 的余弦值.
的余弦值.
某中学将 名高一新生分成水平相同的甲、乙两个“平行班”,每班
名高一新生分成水平相同的甲、乙两个“平行班”,每班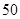 人,吴老师采用
人,吴老师采用 、
、 两种不同的教学方式分别在甲、乙两个班进行教学实验.为了解教学效果,期末考试后,分别从两个班级中各随机抽取
两种不同的教学方式分别在甲、乙两个班进行教学实验.为了解教学效果,期末考试后,分别从两个班级中各随机抽取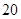 名学生的成绩进行统计,作出的茎叶图如下:
名学生的成绩进行统计,作出的茎叶图如下: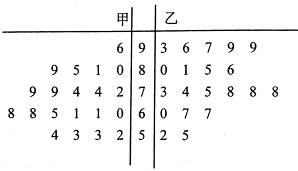
记成绩不低于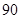 分者为“成绩优秀”.
分者为“成绩优秀”.
(1)在乙班样本的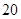 个个体中,从不低于
个个体中,从不低于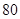 分的成绩中随机抽取
分的成绩中随机抽取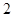 个,记随机变量
个,记随机变量 为抽到“成绩优秀”的个数,求
为抽到“成绩优秀”的个数,求 的分布列及数学期望
的分布列及数学期望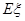 ;
;
(2)由以上统计数据填写下面 列联表,并判断有多大把握认为“成绩优秀”与教学方式有关?
列联表,并判断有多大把握认为“成绩优秀”与教学方式有关?
甲班( 方式) 方式) |
乙班(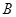 方式) 方式) |
总计 |
|
| 成绩优秀 |
|||
| 成绩不优秀 |
|||
| 总计 |
设函数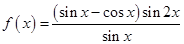 .
.
(1)求 的定义域及最小正周期;
的定义域及最小正周期;
(2)求 的单调递减区间.
的单调递减区间.