如图,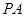 是圆
是圆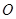 的切线,切点为
的切线,切点为 ,过
,过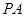 的中点
的中点 作割线交圆
作割线交圆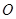 于点
于点 和
和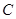 。求证:
。求证:

(本小题共12分)已知函数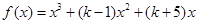 ,其中
,其中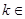
 .
.
(I)若函数 有三个不同零点,求
有三个不同零点,求 的取值范围;
的取值范围;
(II)若函数 在区间
在区间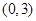 上不是单调函数,求
上不是单调函数,求 的取值范围.
的取值范围.
(本小题共12分)已知曲线 上任意一点P到两个定点F1(-
上任意一点P到两个定点F1(- ,0)和F2(
,0)和F2( ,0)的距离之和为4.
,0)的距离之和为4.
(1)求曲线 的方程;
的方程;
(2)设过(0,-2)的直线 与曲线
与曲线 交于C、D两点,且
交于C、D两点,且 为坐标原点),求直线
为坐标原点),求直线 的方程.
的方程.
(本小题共12分)如图所示,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,
F为CE上的点,且BF⊥平面ACE
(1)求证:AE⊥平面BCE;
(2)求证:AE∥平面BFD;
(本小题共12分)将一颗骰子先后抛掷2次,观察向上的点数,求:
(1)两数之和为5的概率;
(2)两数中至少有一个奇数的概率;
(3)以第一次向上点数为横坐标x,第二次向上的点数为纵坐标y的点(x,y)在圆x2+y2=15的内部的概率.
(本小题共12分)
设函数 的最大值为
的最大值为 ,最小正周期为
,最小正周期为 .
.
(Ⅰ)求 、
、 ;
;
(Ⅱ)若有10个互不相等的正数 满足
满足
求 的值.
的值.