如图，曲线C1是以原点O为中心，F1、F2为焦点的椭圆的一部分，曲线C2是以原点O为顶点，F2为焦点的抛物线的一部分，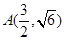
是曲线C1和C2的交点.
(Ⅰ)求曲线C1和C2所在的椭圆和抛物线的方程；
(Ⅱ)过F2作一条与x轴不垂直的直线，分别与曲线C1、C2依次交于B、C、D、E四点，若G为CD中点，H为BE中点，问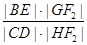
是否为定值，若是，求出定值；若不是，请说明理由.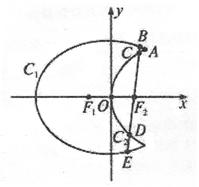
本题共有2个小题，第1小题满分6分，第2小题满分8分．
已知圆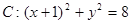
．
（1）求过点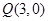
的圆C的切线
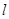的方程；
（2）如图，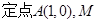
为圆C上一动点，点P在AM上，点N在CM上，且满足
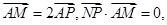求
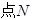的轨迹．
本题共有2个小题，第1小题满分6分，第2小题满分8分．
在二项式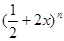
的展开式中：
（1）若第5项，第6项与第7项的二项式系数成等差数列，求展开式中二项式系数最大的项；
（2）若所有项的二项式系数和等于4096，求展开式中系数最大的项．
如图，直线
平面
，
为正方形，
，求直线
与
所成角的大小．
已知函数
，函数
．
（1）若
，求不等式
的解集；
（2）若对任意
,均存在
,使得
成立，求实数
的取值范围．
已知椭圆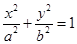
的左焦点
为圆
的圆心，且椭圆上的点到点的距离的最小值为
．
（1）求椭圆的方程；
（2）已知经过点的动直线
与椭圆交于不同的两点
，点
，求
的值．