已知函数 .
.
(1)若不等式 的解集为
的解集为 ,求实数
,求实数 的值;
的值;
(2)在(1)的条件下,若存在实数 使
使 成立,求实数
成立,求实数 的取值范围.
的取值范围.
已知椭圆C: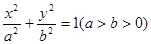 的长轴是短轴的两倍,点
的长轴是短轴的两倍,点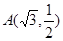 在椭圆上.不过原点的直线l与椭圆相交于A、B两点,设直线OA、l、OB的斜率分别为
在椭圆上.不过原点的直线l与椭圆相交于A、B两点,设直线OA、l、OB的斜率分别为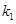 、
、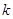 、
、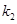 ,且
,且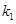 、
、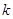 、
、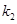 恰好构成等比数列.
恰好构成等比数列.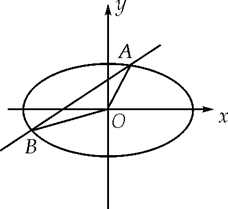
(Ⅰ)求椭圆C的方程.
(Ⅱ)试探究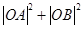 是否为定值?若是,求出这个值;否 则求出它的取值范围.
是否为定值?若是,求出这个值;否 则求出它的取值范围.
已知函数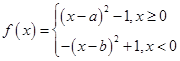 ,其中
,其中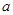 ,
,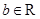 .
.
(Ⅰ)当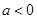 时,且
时,且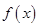 为奇函数,求
为奇函数,求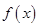 的表达式;
的表达式;
(Ⅱ)当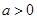 时,且
时,且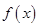 在
在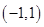 上单调递减,求
上单调递减,求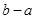 的值.
的值.
如图,正方形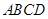 与等边三角形
与等边三角形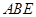 所在的平面互相垂直,
所在的平面互相垂直,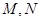 分别是
分别是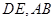 的中点.
的中点.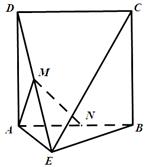
(Ⅰ)证明: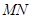 ∥平面
∥平面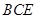 ;
;
(Ⅱ)求二面角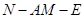 的正切值.
的正切值.
已知函数
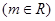 在区间
在区间 上的最大值为
上的最大值为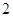 .
.
(Ⅰ)求常数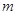 的值;
的值;
(Ⅱ)在 中,角
中,角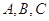 所对的边长分别为
所对的边长分别为 ,若
,若 ,
, ,
, 面积为
面积为 ,求边长
,求边长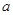 的值.
的值.
(本小题12分)已知函数
(1)求函数f(x)的单调区间;
(2)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,对于任意的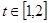 ,函数
,函数 在区间(t,3)上总不是单调函数,求m的取值范围;
在区间(t,3)上总不是单调函数,求m的取值范围;
(3)求证: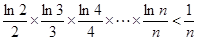 (
( ).
).