已知点H(-3,0),点P在y轴上,点Q在x轴的正半轴上,点M在直线PQ上,且满足 .
.
⑴ 当点P在y轴上移动时,求点M的轨迹G;
⑵ 过点T(-1,0)作直线l与轨迹G交于A、B两点,若在x轴上存在一点E(x0,0),
使得 ABE是等边三角形,求x0的值.
ABE是等边三角形,求x0的值.
包含甲在内的甲、乙、丙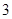 个人练习传球,设传球
个人练习传球,设传球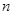 次,每人每次只能传一下,首先从甲手中传出,第
次,每人每次只能传一下,首先从甲手中传出,第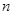 次仍传给甲,共有多少种不同的方法?
次仍传给甲,共有多少种不同的方法?
为了解决上述问题,设传球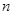 次,第
次,第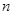 次仍传给甲的传球方法种数为
次仍传给甲的传球方法种数为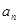 ;设传球
;设传球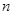 次,第
次,第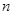 次不传给甲的传球方法种数为
次不传给甲的传球方法种数为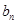 .根据以上假设回答下列问题:
.根据以上假设回答下列问题:
(1)求出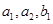 的值;
的值;
(2)根据你的理解写出 与
与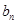 的关系式;
的关系式;
(3)求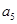 的值及通项公式
的值及通项公式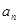 .
.
已知函数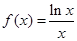 .
.
(1)求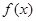 在点
在点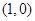 处的切线方程;
处的切线方程;
(2)求函数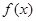 在
在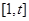 上的最大值.
上的最大值.
已知函数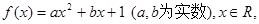
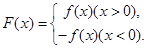
(1)若不等式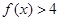 的解集为
的解集为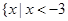 或
或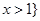 ,求
,求 的表达式;
的表达式;
(2)在(1)的条件下, 当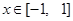 时,
时, 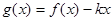 是单调函数, 求实数k的取值范围;
是单调函数, 求实数k的取值范围;
(3)设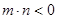 ,
, 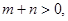
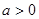 且
且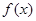 为偶函数, 判断
为偶函数, 判断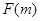 +
+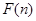 能否大于零?
能否大于零?
设函数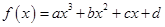 (a>0),且方程
(a>0),且方程 (x)-9x=0的两个根分别为1,4.
(x)-9x=0的两个根分别为1,4.
(1)当a=3且曲线y="f" (x)过原点时,求f (x)的解析式;
(2)若f (x)在(-∞,+∞)内无极值点,求a的取值范围.
){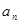 }、{
}、{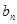 }都是各项为正的数列,对任意的
}都是各项为正的数列,对任意的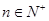 ,都有
,都有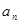 、
、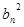 、
、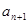 成等差数列,
成等差数列,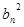 、
、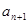 、
、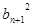 成等比数列.
成等比数列.
(1) 试问{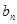 }是否为等差数列,为什么?
}是否为等差数列,为什么?
(2) 如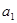 =1,
=1,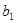 =
=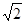 ,求
,求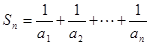 ;
;