已知椭圆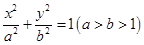 内有圆
内有圆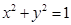 ,如果圆的切线与椭圆交A、B两点,且满足
,如果圆的切线与椭圆交A、B两点,且满足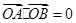 (其中
(其中 为坐标原点).
为坐标原点).
(1)求证: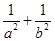 为定值;
为定值;
(2)若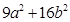 达到最小值,求此时的椭圆方程;
达到最小值,求此时的椭圆方程;
(3)在满足条件(2)的椭圆上是否存在点P,使得从P向圆所引的两条切线互相垂直,如果存在,求出点的坐标,如果不存在,说明理由.
在直角坐标系
中,曲线
的参数方程为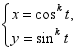 为参数
.以坐标原点为极点,
轴正半轴为极轴建立极坐标系,曲线
的极坐标方程为
.
为参数
.以坐标原点为极点,
轴正半轴为极轴建立极坐标系,曲线
的极坐标方程为
.
(1)当 时, 是什么曲线?
(2)当 时,求 与 的公共点的直角坐标.
已知A、B分别为椭圆E: (a>1)的左、右顶点,G为E的上顶点, ,P为直线x=6上的动点,PA与E的另一交点为C,PB与E的另一交点为D.
(1)求E的方程;
(2)证明:直线CD过定点.
已知函数 .
(1)当 时,讨论 的单调性;
(2)若 有两个零点,求 的取值范围.
如图, 为圆锥的顶点, 是圆锥底面的圆心, 是底面的内接正三角形, 为 上一点,∠ APC=90°.
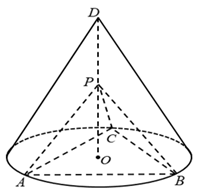
(1)证明:平面 PAB⊥平面 PAC;
(2)设 DO= ,圆锥的侧面积为 ,求三棱锥 P− ABC的体积.
的内角A,B,C的对边分别为a,b,c.已知B=150°.
(1)若a= c,b=2 ,求 的面积;
(2)若sinA+ sinC= ,求C.