、如图,在三棱锥P-ABC中,PA⊥底面ABC,△ABC为正三角形,D、E分别是BC、CA的中点。
(Ⅰ) 若PA=AB=2,求三棱锥P-ABC的体积;
(Ⅱ)证明:BE⊥平面PAC
(Ⅲ)如何在BC上找一点F,使AD//平面PEF?并说明理由。
如图,四棱锥P-ABCD的底面是矩形,侧面PAD丄底面ABCD,. .
.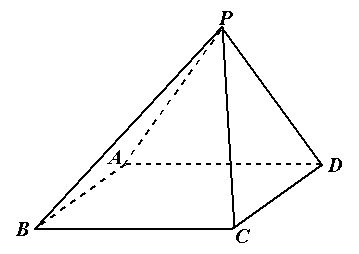
(1)求证:平面PAB丄平面PCD
(2)如果AB=BC=2,PB=PC=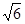 求四棱锥P-ABCD的体积.
求四棱锥P-ABCD的体积.
设直线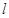 的方程为
的方程为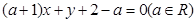 .
.
(1)若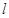 在两坐标轴上的截距相等,求
在两坐标轴上的截距相等,求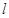 的方程;
的方程;
(2)若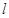 不经过第二象限,求实数
不经过第二象限,求实数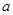 的取值范围。
的取值范围。
已知过曲线 上任意一点
上任意一点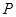 作直线
作直线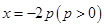 的垂线,垂足为
的垂线,垂足为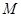 ,且
,且 .
.
⑴求曲线 的方程;
的方程;
⑵设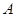 、
、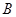 是曲线
是曲线 上两个不同点,直线
上两个不同点,直线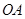 和
和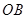 的倾斜角分别为
的倾斜角分别为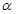 和
和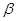 ,当
,当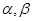 变化且
变化且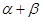 为定值
为定值 时,证明直线
时,证明直线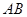 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
已知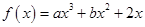 在
在 处取得极值,且在点
处取得极值,且在点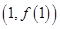 处的切线斜率为
处的切线斜率为 .
.
⑴求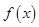 的单调增区间;
的单调增区间;
⑵若关于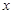 的方程
的方程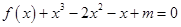 在区间
在区间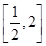 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数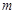 的取值范围.
的取值范围.
已知四棱锥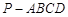 的底面为直角梯形,
的底面为直角梯形,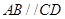 ,
,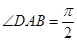 ,
,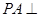 底面
底面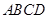 ,且
,且 ,
, 是
是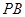 的中点.
的中点.
⑴求证:直线 平面
平面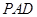 ;
;
⑵若直线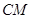 与平面
与平面 所成的角为
所成的角为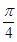 ,求四棱锥
,求四棱锥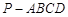 的体积.
的体积.