(本小题共13分)已知椭圆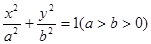 的右焦点为
的右焦点为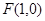 ,
, 为椭圆的上顶点,
为椭圆的上顶点,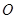 为坐标原点,且△
为坐标原点,且△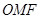 是等腰直角三角形.
是等腰直角三角形.
(Ⅰ)求椭圆的方程;
(Ⅱ)是否存在直线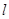 交椭圆于
交椭圆于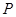 ,
,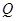 两点, 且使点
两点, 且使点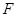 为△
为△ 的垂心(垂心:三角形三边高线的交点)?若存在,求出直线
的垂心(垂心:三角形三边高线的交点)?若存在,求出直线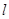 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
从8名运动员中选4人参加4×100米接力赛,在下列条件下,各有多少种不同的排法?(用数字结尾)
(1)甲、乙两人必须跑中间两棒;
(2)若甲、乙两人只有一人被选且不能跑中间两棒;
(3)若甲、乙两人都被选且必须跑相邻两棒.
已知函数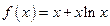 .
.
(1)求函数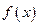 的图像在点
的图像在点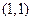 处的切线方程;
处的切线方程;
(2)若 ,且
,且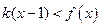 对任意
对任意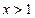 恒成立,求
恒成立,求 的最大值;
的最大值;
(3)当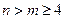 时,证明
时,证明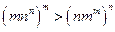 .
.
如图,已知直线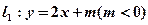 与抛物线
与抛物线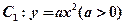 和圆
和圆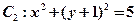 都相切,
都相切,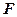 是
是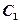 的焦点.
的焦点.
(1)求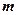 与
与 的值;
的值;
(2)设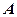 是
是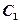 上的一动点,以
上的一动点,以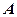 为切点作抛物线
为切点作抛物线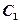 的切线
的切线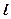 ,直线
,直线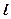 交
交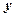 轴于点
轴于点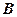 ,以
,以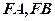 为邻边作平行四边形
为邻边作平行四边形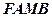 ,证明:点
,证明:点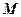 在一条定直线上;
在一条定直线上;
(3)在(2)的条件下,记点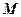 所在的定直线为
所在的定直线为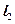 ,直线
,直线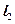 与
与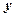 轴交点为
轴交点为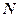 ,连接
,连接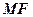 交抛物线
交抛物线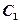 于
于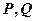 两点,求
两点,求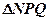 的面积
的面积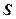 的取值范围.
的取值范围.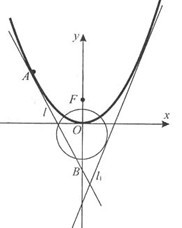
(如图,已知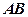
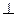 平面
平面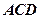 ,
,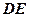 ∥
∥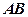 ,
,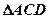 是正三角形,
是正三角形,
且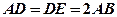 .
.
(1)设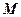 是线段
是线段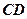 的中点,求证:
的中点,求证: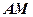 ∥平面
∥平面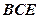 ;
;
(2)求直线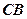 与平面
与平面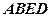 所成角的余弦值.
所成角的余弦值.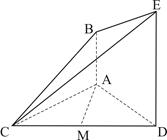
已知数列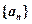 满足
满足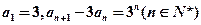 ,数列
,数列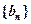 满足
满足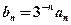 .
.
(1)求证:数列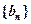 是等差数列;
是等差数列;
(2)设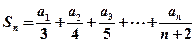 ,求满足不等式
,求满足不等式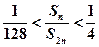 的所有正整数
的所有正整数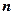 的值.
的值.