已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,现学校决定利用随机数表法从中抽取100人进行成绩抽样调查,先将800人按001,002, ,800进行编号;
(1)如果从第8行第7列的数开始向右读,请你依次写出最先检查的3个人的编号;
(下面摘取了第7行到第9行)
(2)抽取的100的数学与地理的水平测试成绩如下表:
成绩分为优秀、良好、及格三个等级;横向,纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有20+18+4=42,若在该样本中,数学成绩优秀率是30%,求a,b的值:
| 人数 |
数学 |
|||
| 优秀 |
良好 |
及格 |
||
| 地理 |
优秀 |
7 |
20 |
5 |
| 良好 |
9 |
18 |
6 |
|
| 及格 |
a |
4 |
b |
(3)在地理成绩及格的学生中,已知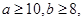 求数学成绩为优秀的人数比及格的人数少的概率.
求数学成绩为优秀的人数比及格的人数少的概率.
(本小题满分14分)已知 ,若函数
,若函数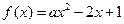 在区间
在区间 上
上
的最大值为 ,最小值为
,最小值为 ,令
,令 .
.
(1)求 的函数表达式;
的函数表达式;
(2)判断函数 在区间
在区间 上的单调性,并求出
上的单调性,并求出 的最小值.
的最小值.
(本小题满分14分)已知直线 :y=k(x+2
:y=k(x+2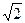 )与圆O:x2+y2=4相交于不重合的
)与圆O:x2+y2=4相交于不重合的
A、B两点,O是坐标原点,且三点A、B、O构成三角形.
(1)求k的取值范围;
(2)三角形ABO的面积为S,试将S表示成k的函数,并求出它的定义域;
(3)求S的最大值,并求取得最大值时k的值.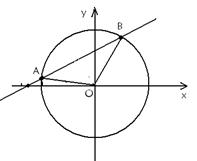
.(本小题满分14分)电视台应某企业之约播放两套连续剧.其中,连续剧甲每次播放时间为80min,其中广告时间为1min,收视观众为60万;连续剧乙每次播放时间为40min,其中广告时间为1min,收视观众为20万.已知此企业与电视台达成协议,要求电视台每周至少播放6min广告,而电视台每周只能为该企业提供不多于320min的节目时间(此时间不包含广告).如果你是电视台的制片人,电视台每周播映两套连续剧各多少次,才能获得最高的收视率?
(本小题满分12分)已知等差数列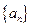 满足:
满足: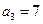 ,
,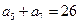 ,
,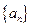 的前n项和为
的前n项和为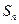 .
.
(Ⅰ)求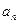 及
及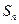 ;
;
(Ⅱ)令bn=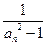 (
(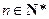 ),求数列
),求数列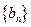 的前n项和
的前n项和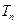 .
.
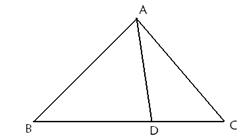
(本小题满分12分) 在△ABC中,已知B=45°,D是BC边上的一点,AD="10," AC=14,DC=6,求AB的长.