（本小题满分14分）
已知A（-1，2）为抛物线C: y=2x2上的点，直线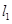
过点A，且与抛物线C 相切，直线
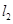:x=a(a≠-1)交抛物线C于B，交直线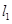于点D.
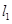（1）求直线的方程.
（2）设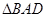
的面积为S1，求
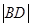及S1的值.
（3）设由抛物线C，直线
所围成的图形的面积为S2，求证S1:S2的值为与a无关的常数.
（本小题满分12分）如图，在正三棱柱
中，
分别是
的中点,
．
（Ⅰ）在棱
上是否存在点
使
？如果存在，试确定它的位置；如果不存在，请说明理由；
（Ⅱ）求截面
与底面
所成锐二面角的正切值；
（Ⅲ）求点
到截面的距离．
（本小题满分12分）甲、乙两篮球运动员进行定点投篮，每人各投4个球，甲投篮命中的概率为
，乙投篮命中的概率为
．
（Ⅰ）求甲至多命中2个且乙至少命中
2个的概率；
（Ⅱ）若规定每投蓝一次命中得3分，未命中得-1分，求乙所得分数
的概率分布和数学期望．
（本小题满分12分）在直角坐标平面内，已知点
，其中
．
（Ⅰ）若
，求角
的弧度数；
（Ⅱ）若
，求
的值．
23．（本小题满分10分）
将一枚硬币连续抛掷
次，每次抛掷互不影响. 记正面向上的次数为奇数的概率为
，正面向上的次数为偶数的概率为
.
（Ⅰ）若该硬币均匀，试求与；
（Ⅱ）若该硬币有暇疵，且每次正面向上的概率为
，试比较与的大小.
22．（本小题满分10分）
已知动圆
过点
且与直线
相切.
（Ⅰ）求点的轨迹
的方程；
（Ⅱ）过点
作一条直线交轨迹于
两点，轨迹在两点处的切线相交于点
，
为线段
的中点，求证：
轴.