已知函数 ,其中常数a>0.
,其中常数a>0.
(I )当a>2时,求函数f(x)的单调递增区间;
(II)当a=4时,给出两类直线: 与
与 ,其中m,n为常数.判断这两类直线中是否存在
,其中m,n为常数.判断这两类直线中是否存在 的切线?若存在,求出相应的m或n的值;若不存在,说明理由;
的切线?若存在,求出相应的m或n的值;若不存在,说明理由;
(III)设定义在D上的函数 在点
在点 处的切线方程为
处的切线方程为 ,当
,当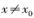 时,若
时,若 在D内恒成立,则称P为函数
在D内恒成立,则称P为函数 的“类对称点”.当a=4时,试问
的“类对称点”.当a=4时,试问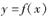 是否存在“类对称点”?若存在,请至少求出一个“类对称点”的横坐标;若不存在,说明理由.
是否存在“类对称点”?若存在,请至少求出一个“类对称点”的横坐标;若不存在,说明理由.
曲线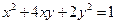 在二阶矩阵
在二阶矩阵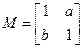 的作用下变换为曲线
的作用下变换为曲线 ,①求实数
,①求实数 的值;②求
的值;②求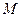 的逆矩阵
的逆矩阵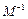 .
.
已知函数 上是增函数.(I)求实数a的取值范围;(II)在(I)的结论下,设
上是增函数.(I)求实数a的取值范围;(II)在(I)的结论下,设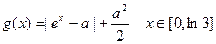 ,求函数
,求函数 的最小值.
的最小值.
如图,已知直线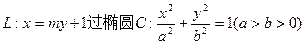 的右焦点F,且交椭圆C于A,B两点,点A,F,B在直线
的右焦点F,且交椭圆C于A,B两点,点A,F,B在直线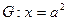 上的射影依次为点D,K,E.
上的射影依次为点D,K,E.
(1)若抛物线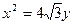 的焦点为椭圆C的上顶点,求椭圆C的方程; (2)对于(1)中的椭圆C,若直线L交y轴于点M,且
的焦点为椭圆C的上顶点,求椭圆C的方程; (2)对于(1)中的椭圆C,若直线L交y轴于点M,且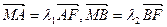 ,当m变化时,求
,当m变化时,求 的值;(3)连接AE,BD,试探索当m变化时,直线AE、BD是否相交于一定点N?若交于定点N,请求出N点的坐标并给予证明;否则说明理由.
的值;(3)连接AE,BD,试探索当m变化时,直线AE、BD是否相交于一定点N?若交于定点N,请求出N点的坐标并给予证明;否则说明理由.
如图,已知两个正方形ABCD 和DCEF不在同一平面内,M,N分别为AB,DF的中点。(1)若平面ABCD ⊥平面DCEF,求直线MN与平面DCEF所成角的正弦值;
(2)用反证法证明:直线ME 与 BN 是两条异面直线

已知向量 且A、B、C分别为△ABC的三边a、b、c所对的角
且A、B、C分别为△ABC的三边a、b、c所对的角
(1)求角C的大小;(2)若 ,求c边的长。
,求c边的长。