已知函数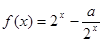 (
(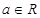 ),将
),将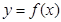 的图象向右平移两个单位,得到函数
的图象向右平移两个单位,得到函数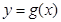 的图象,函数
的图象,函数 与函数
与函数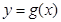 的图象关于直线
的图象关于直线 对称.
对称.
(1)求函数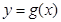 和
和 的解析式;
的解析式;
(2)若方程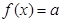 在
在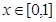 上有且仅有一个实根,求
上有且仅有一个实根,求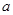 的取值范围;
的取值范围;
(3)设 ,已知
,已知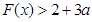 对任意的
对任意的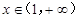 恒成立,求
恒成立,求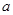 的取值范围.
的取值范围.
(本小题满分14分)
已知数列 的前
的前 项和
项和 满足
满足 ,等差数列
,等差数列 满足
满足 ,
, 。
。
(1)求数列 、
、 的通项公式;
的通项公式;
(2)设 ,数列
,数列 的前
的前 项和为
项和为 ,问
,问 >
> 的最小正整数
的最小正整数 是多少?
是多少?
(本小题满分14分)
如图的几何体中, 平面
平面 ,
,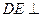 平面
平面 ,△
,△ 为等边三角形
为等边三角形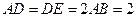 ,
, 为
为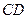 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求证:平面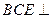 平面
平面 。
。
(本小题满分12分)
甲、乙二名射击运动员参加今年深圳举行的第二十六届世界大学生夏季运动会的预选赛,他们分别射击了4次,成绩如下表(单位:环):
| 甲 |
5 |
6 |
9 |
10 |
| 乙 |
6 |
7 |
8 |
9 |
(1)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;
(2)现要从中选派一人参加决赛,你认为选派哪位运动员参加比较合适?请说明理由.
(本小题满分12分)
设三角形 的内角
的内角 的对边分别为
的对边分别为
 ,
, .
.
(1)求 边的长;
边的长;
(2)求角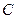 的大小。
的大小。
设等比数列{ }的前
}的前 项和
项和 ,首项
,首项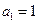 ,公比
,公比 .
.
(Ⅰ)证明: ;
;
(Ⅱ)若数列{ }满足
}满足 ,
, ,求数列{
,求数列{ }的通项公式;
}的通项公式;
(Ⅲ)若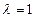 ,记
,记 ,数列{
,数列{ }的前项和为
}的前项和为 ,求证:当
,求证:当 时,
时, .
.