已知定义在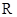 上的函数
上的函数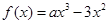 ,其中
,其中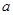 为大于零的常数.
为大于零的常数.
(Ⅰ)当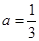 时,令
时,令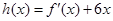 ,求证:当
,求证:当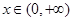 时,
时,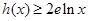 (
(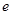 为自然对数的底数);
为自然对数的底数);
(Ⅱ)若函数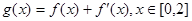 ,在
,在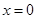 处取得最大值,求
处取得最大值,求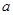 的取值范围.
的取值范围.
如图,四边形PDCE为矩形,ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD= .
.
(Ⅰ)若M为PA中点,求证:AC∥平面MDE;
(Ⅱ)求平面PAD与PBC所成锐二面角的大小.
已知函数 满足
满足 ,当
,当 时
时 ;当
;当 时
时 .
.
(Ⅰ)求函数 在(-1,1)上的单调区间;
在(-1,1)上的单调区间;
(Ⅱ)若 ,求函数
,求函数 在
在 上的零点个数.
上的零点个数.
在 中,
中, 分别为角
分别为角 的对边,
的对边, 的面积S满足
的面积S满足
(Ⅰ)求角A的值;
(Ⅱ)若 ,设角B的大小为x,用x表示c,并求c的取值范围.
,设角B的大小为x,用x表示c,并求c的取值范围.
已知函数f(x)=|x-2|,g(x)=-|x+3|+m.
(1)解关于x的不等式f(x)+a-1>0(a∈R);
(2)若函数f(x)的图象恒在函数g(x)图象的上方,求m的取值范围.
已知直线l经过点 ,倾斜角α=
,倾斜角α= ,圆C的极坐标方程为
,圆C的极坐标方程为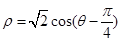 .
.
(1)写出直线l的参数方程,并把圆C的方程化为直角坐标方程;
(2)设l与圆C相交于两点A、B,求点P到A、B两点的距离之积.